均匀分布简介
均匀分布是a到b区间内的每个值出现的概率相同的概率分布。
如果随机变量X服从均匀分布,则X取x 1和x 2之间的值的概率可以通过以下公式求出:
P(x 1 < X < x 2 ) = (x 2 – x 1 ) / (b – a)
金子:
- x 1 :较低的利息值
- x 2 :利息上限值
- a:最小可能值
- b:最大可能值
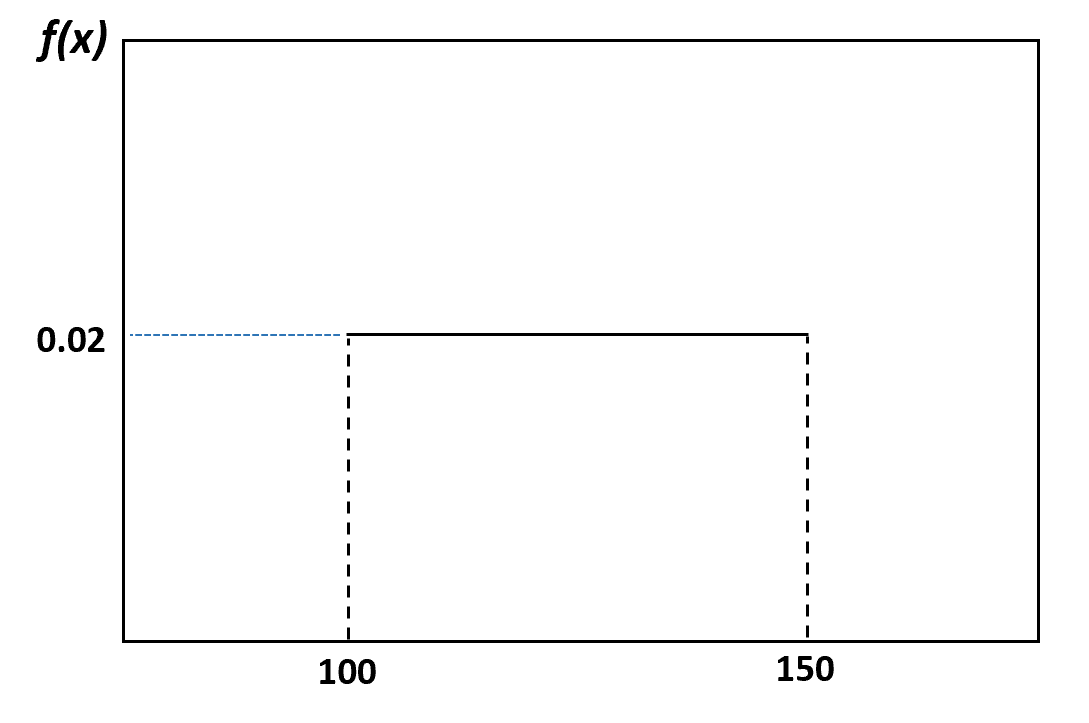
例如,假设海豚的体重均匀分布在 100 到 150 磅之间。
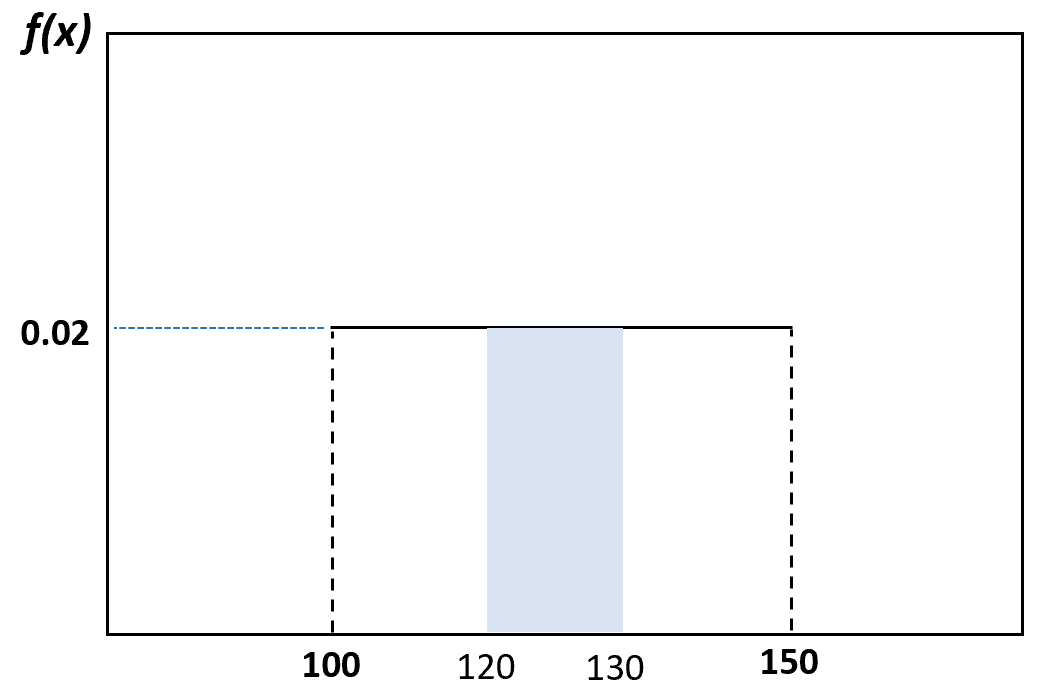
如果我们随机选择一只海豚,我们可以使用上面的公式来确定所选海豚体重在 120 到 130 磅之间的概率:
- P(120 < X < 130) = (130 – 120) / (150 – 100)
- P(120 < X < 130) = 10/50
- P(120 < X < 130) = 0.2
所选海豚体重在 120 到 130 磅之间的概率是0.2 。
可视化均匀分布
如果我们创建密度图来可视化均匀分布,它将如下图所示:
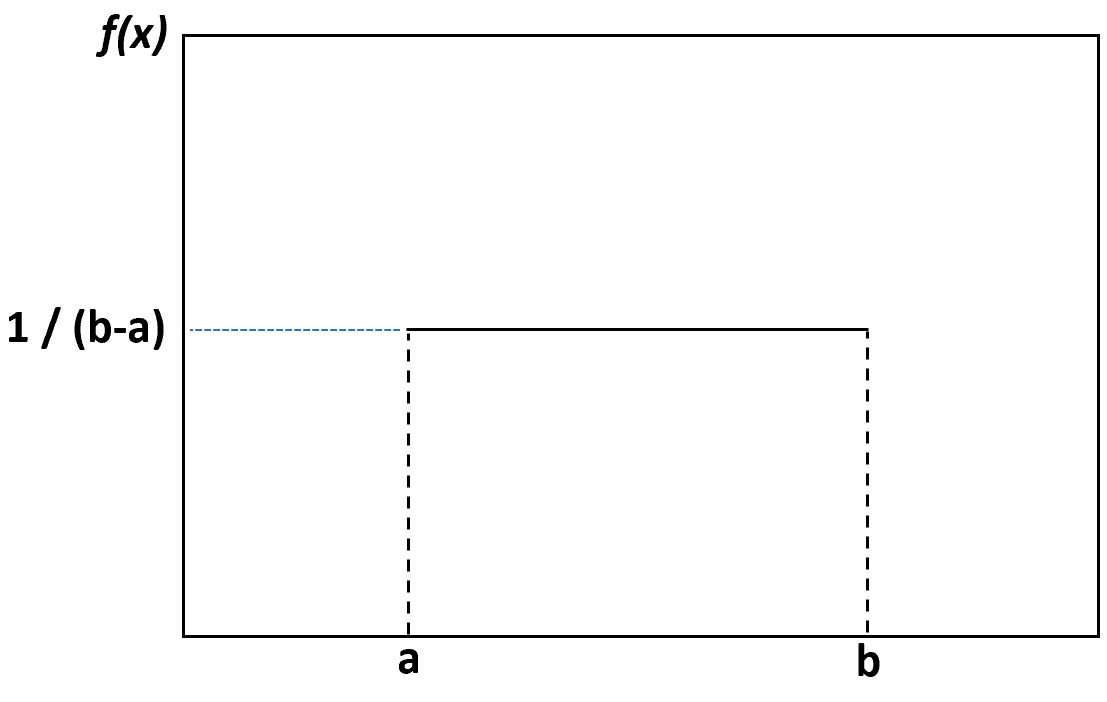
下限a和上限b之间的每个值都具有相同的出现概率,并且超出这些限制的任何值的概率为零。
例如,在前面的例子中,我们说海豚的体重均匀分布在 100 到 150 磅之间。以下是如何可视化此分布的方法:
随机选择的海豚体重在 120 到 130 磅之间的概率可以如下可视化:
均匀分布的性质
均匀分布具有以下性质:
- 平均值: (a + b) / 2
- 中位数: (a + b) / 2
- 标准差:√ (b – a) 2 / 12
- 差值: (b – a) 2 / 12
例如,假设海豚的体重均匀分布在 100 到 150 磅之间。
我们可以计算该分布的以下属性:
- 平均重量:(a+b)/2=(150+100)/2= 125
- 中位权重:(a + b) / 2 = (150 + 100) / 2 = 125
- 重量标准差:√ (150 – 100) 2 / 12 = 14.43
- 重量变化:(150 – 100) 2 / 12 = 208.33
统一分配实践的问题
使用以下练习题来测试您对均匀分布的了解。
问题1:每20分钟就有一辆公交车到一个公交车站。如果您到达公交车站,公交车在 8 分钟或更短时间内到达的概率是多少?
方案一:最短等待时间为0分钟,最长等待时间为20分钟。利息下限为 0 分钟,利息上限为 8 分钟。
因此,我们将计算概率如下:
P(0 < X < 8) = (8-0) / (20-0) = 8/20 = 0.4 。
问题2:一场NBA比赛的时长均匀分布在120到170分钟之间。随机选择的一场 NBA 比赛持续时间超过 155 分钟的概率是多少?
方案2:最短时长为120分钟,最长时长为170分钟。利息下限为 155 分钟,利息上限为 170 分钟。
因此,我们将计算概率如下:
P(155 < X < 170) = (170-155) / (170-120) = 15/50 = 0.3 。
问题3:某种青蛙的体重均匀分布在15克到25克之间。如果你随机选择一只青蛙,它的重量在 17 到 19 克之间的概率是多少?
方案3:最小重量为15克,最大重量为25克。利息下限为17克,利息上限为19克。
因此,我们将计算概率如下:
P(17 < X < 19) = (19-17) / (25-15) = 2/10 = 0.2 。
注意:我们可以使用均匀分布计算器来检查每个问题的答案。