基尼指数（或基尼系数）

本文解释什么是基尼指数（也称为基尼系数）及其用途。此外，您还将找到有关如何查找基尼指数的已解决练习。最后，您将能够看到该统计指标的解释以及基尼指数和洛伦兹曲线之间的关系。

什么是基尼指数？

基尼指数，也称为基尼系数，是用来衡量一个地区收入不平等程度的统计值。换句话说，基尼指数表明一个地区在其人口中收入分配的平等程度。

基尼指数是一个介于0和1之间的数字。如果基尼指数为0，这意味着该领土内的收入分配尽可能公平（完全平等），或者换句话说，所有居民都有相同的收入。另一方面，当基尼系数为1时，这相当于完全不平等，也就是说一个人拥有该领土的所有收入，而其他人则一无所获。

基尼指数用于比较世界不同国家之间的经济状况，因为它可以比较收入分配最平等的国家，反之亦然，比较最不平等的国家。

基尼指数是由著名统计学家科拉多·基尼发明的，因而得名。

如何计算基尼指数

给定基尼指数（或基尼系数）的定义，以下是该统计指标的计算方法。

基尼指数（或基尼系数）的计算公式如下：

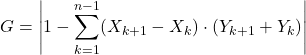
金子：

• 

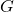
  是基尼指数。

• 

  是变量总体的累积比例。

• 

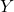
  是收入变量的累计比例。

为了让您能够准确地了解基尼指数是如何确定的，下面给出了一个分步示例：

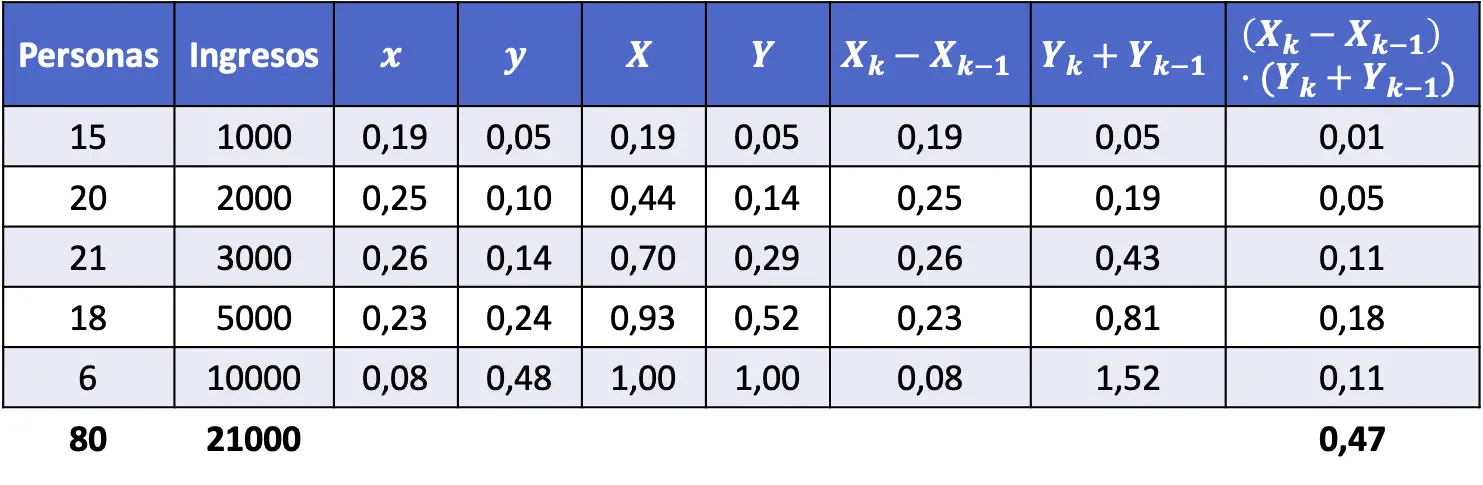
• 计算下表所示收入人口的基尼指数。

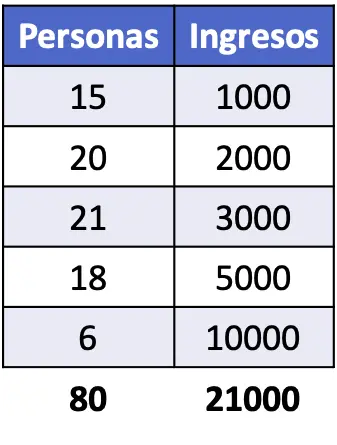
为了求出基尼系数，我们需要确定每个收入水平所占的比例以及累计比例。此外，必须执行公式中给出的计算才能找到基尼指数的值。

简而言之，应将以下列添加到数据表中：

我们现在使用基尼指数公式：

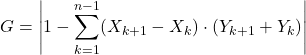
最后，我们将数据代入代数表达式并计算基尼系数：

基尼指数与洛伦兹曲线的关系

在本节中，我们将了解基尼指数（也称为基尼系数）与洛伦兹曲线的关系。

洛伦兹曲线是一个地区人口经济不平等的图形表示。因此，洛伦兹曲线直观地表明了人口的经济不平等程度。

另一方面，正如我们所看到的，基尼指数是一个用于数字描述人口不平等的值。

因此，基尼指数和洛伦兹曲线具有相同的目标：两者都用于确定领土居民之间的经济不平等。然而，基尼指数以数字方式评估收入不平等，而洛伦兹曲线则以图形方式分析经济不平等。

另外，基尼指数可以根据洛伦兹曲线所限定的区域，按照以下公式计算：

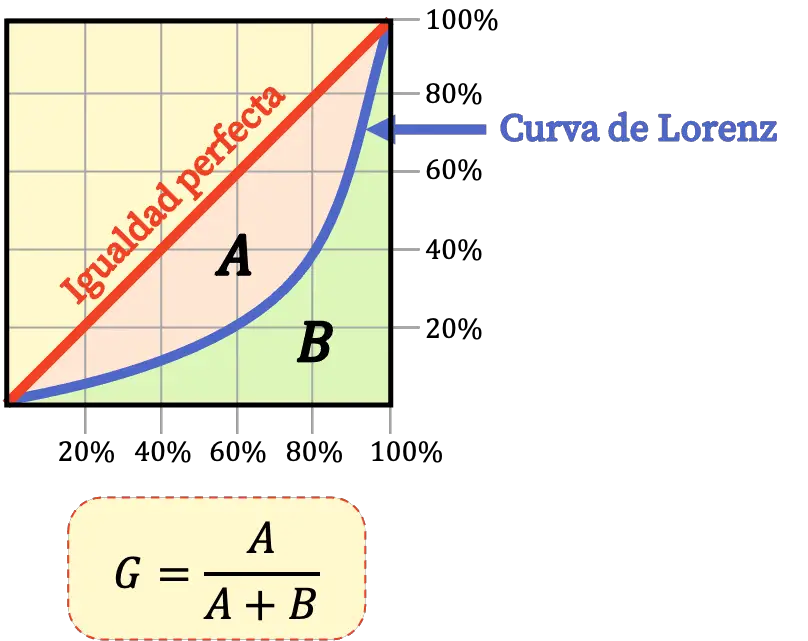
基尼指数解读

基尼指数的值可以在 0 到 1 之间（包括 0 和 1）。基尼系数的值越接近0，意味着该地区的经济更加平等。另一方面，基尼指数越高，一个地区居民之间收入分配的不平等程度就越大。

因此，在所有居民收入完全相同的最佳情况下，基尼指数将等于零。相反，当领土呈现完全不平等时，即一个居民获得所有收入而其他居民没有收入时，基尼指数将为1。

因此，收入平等程度较高的国家是基尼指数较低的国家。最不平等的国家的基尼指数非常高。

正如我们所看到的，基尼指数与洛伦兹曲线相关。因此，基尼指数越低，洛伦兹曲线就越接近完全平等线。基尼指数越高，基尼曲线的曲率就越大，因此，它距离代表完全平等的线就越远。