多项式分布简介
多项分布描述了当每个结果具有固定的发生概率时,获得k 个不同结果的特定计数的概率。
如果一个随机变量_可以通过下面的公式求得:
概率= n! * (p 1 x 1 * p 2 x 2 * … * p k x k ) / (x 1 !* x 2 ! … * x k !)
金子:
- n:事件总数
- x 1 :结果 1 出现的次数
- p 1 :在给定试验中结果 1 发生的概率
例如,假设一个瓮中有 5 个红色弹珠、3 个绿色弹珠和 2 个蓝色弹珠。如果我们从瓮中随机抽取 5 个弹珠,进行放回,恰好获得 2 个红色弹珠、2 个绿色弹珠和 1 个蓝色弹珠的概率是多少?
为了回答这个问题,我们可以使用具有以下参数的多项分布:
- 人数:5
- x 1 (# 红色弹珠)= 2, x 2 (# 绿色弹珠)= 2, x 3 (# 蓝色弹珠)= 1
- p 1 (红色概率)= 0.5, p 2 (绿色概率)= 0.3, p 3 (蓝色概率)= 0.2
将这些数字代入公式,我们发现概率为:
概率=5! * (.5 2 * .3 2 * .2 1 ) / (2!* 2!* 1!) = 0.135 。
多项式分布练习题
使用以下练习题来测试您对多项分布的了解。
注意:我们将使用多项分布计算器来计算这些问题的答案。
问题1
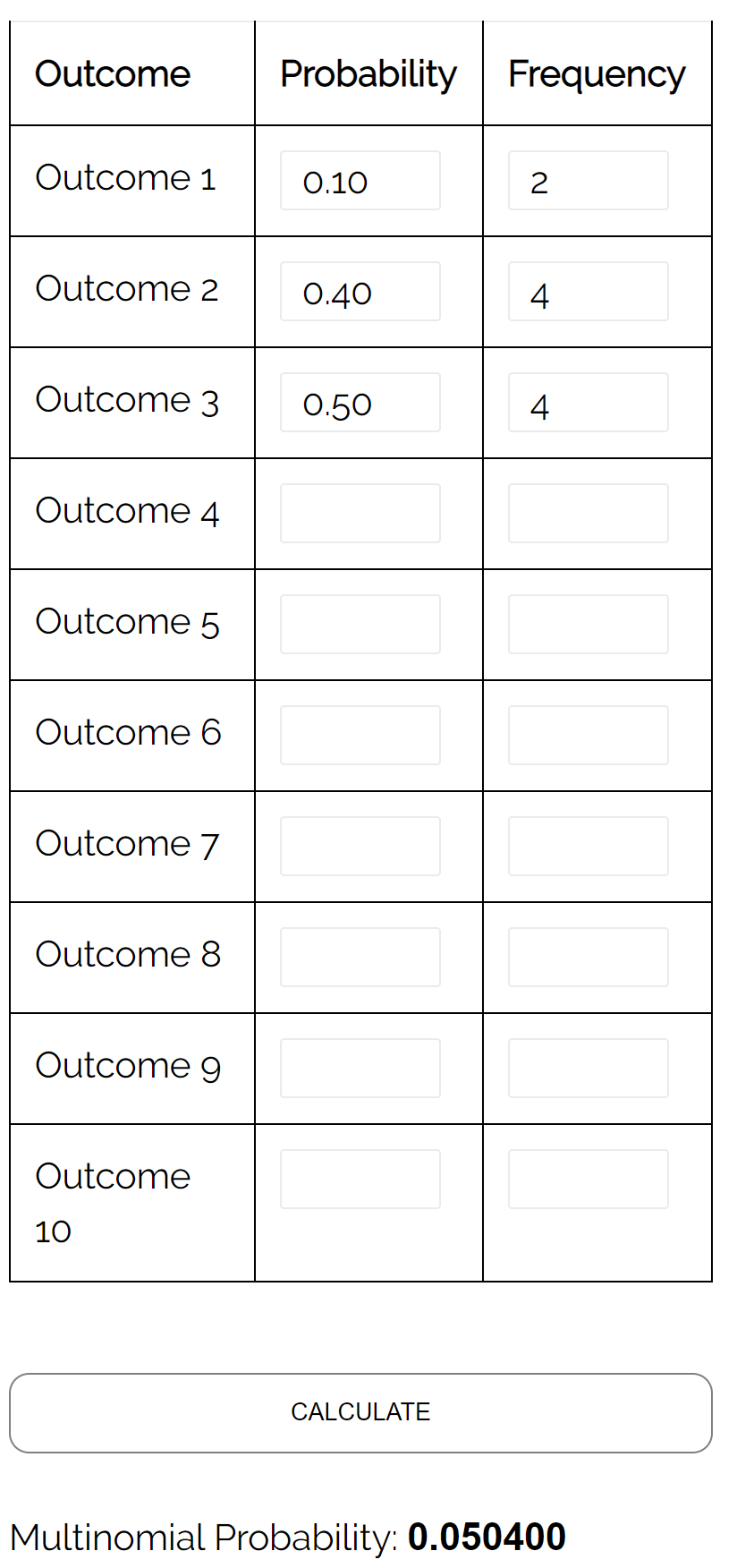
问题:在市长三选一选举中,候选人 A 获得 10% 的选票,候选人 B 获得 40% 的选票,候选人 C 获得 50% 的选票。如果我们随机抽取 10 名选民,那么 2 人投票给候选人 A、4 人投票给候选人 B、4 人投票给候选人 C 的概率是多少?
答案:使用具有以下输入的多项分布计算器,我们发现概率为0.0504:
问题2
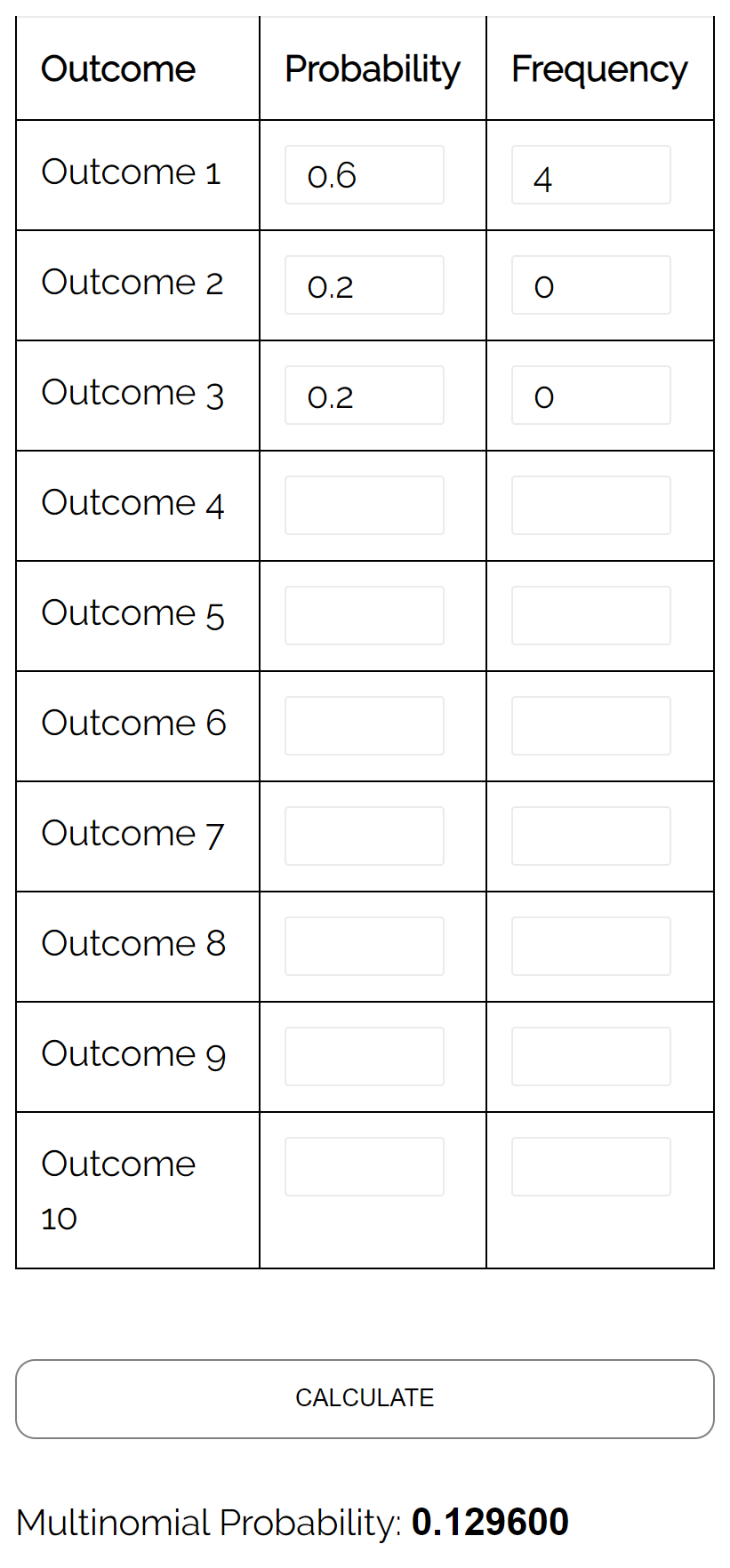
问题:假设一个瓮中有 6 个黄色弹珠、2 个红色弹珠和 2 个粉色弹珠。如果我们从瓮中随机选择 4 个球,进行放回,那么这 4 个球都是黄色的概率是多少?
答案:使用具有以下输入的多项分布计算器,我们发现概率为0.1296:
问题3
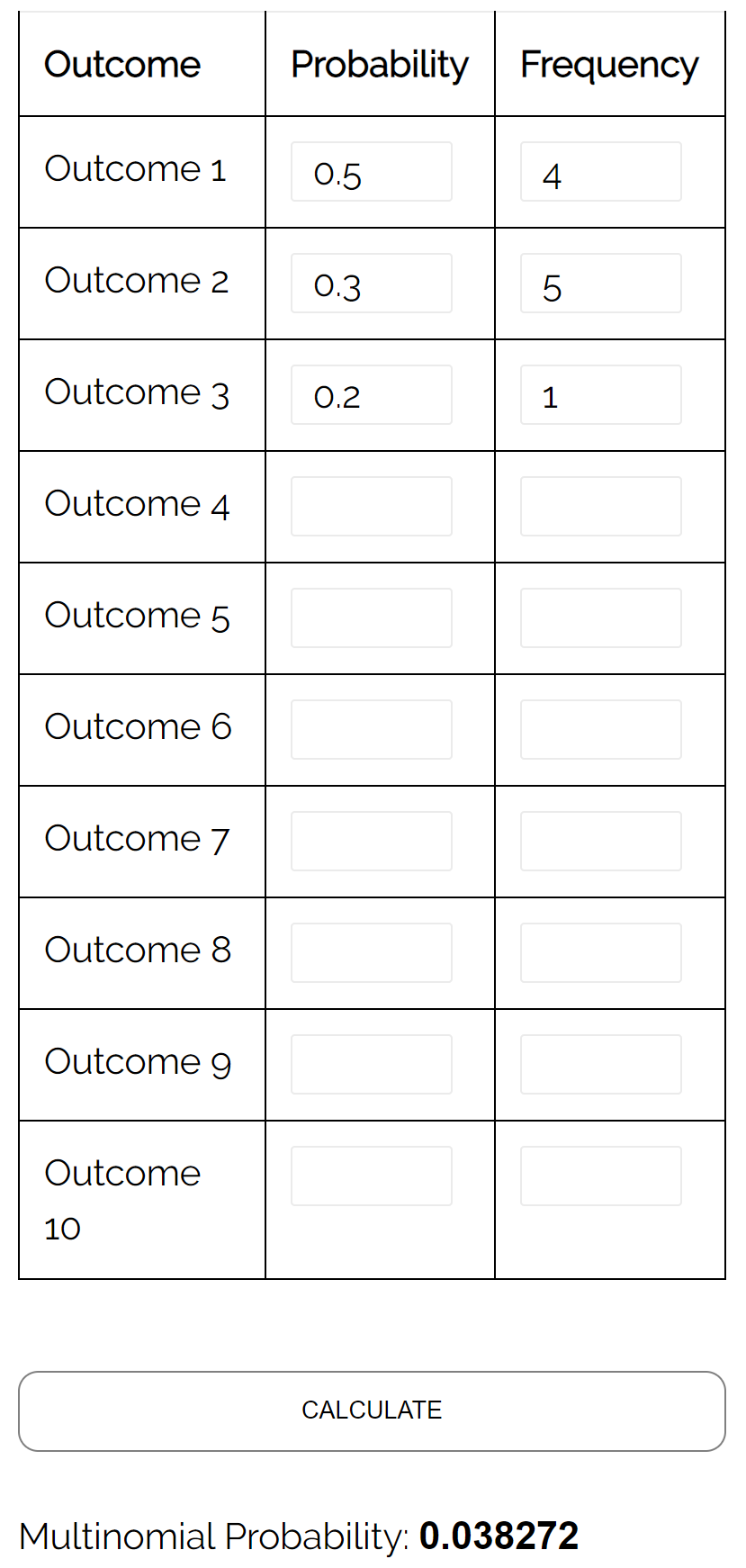
问题:假设两个学生正在互相下棋。学生 A 在给定游戏中获胜的概率为 0.5,学生 B 在给定游戏中获胜的概率为 0.3,在给定游戏中出现平局的概率为 0, 2。如果他们玩 10 场比赛,那么玩家 A 获胜 4 次、玩家 B 获胜 5 次、平局 1 次的概率是多少?
答案:使用具有以下输入的多项分布计算器,我们发现概率为0.038272:
其他资源
以下教程提供了统计中其他常见分布的介绍: