多项分布
本文解释了统计学中的多项分布是什么。因此,您将找到多项分布的定义、其公式是什么、已解决的练习以及此类概率分布的属性是什么。此外,您将能够使用在线计算器计算多项分布的概率。
什么是多项分布?
多项式分布(或多项式分布)是一种概率分布,描述了经过多次试验后,若干互斥事件发生给定次数的概率。
也就是说,如果一个随机实验可以产生三个或更多的排他事件,并且每个事件单独发生的概率已知,则使用多项分布来计算当进行多个实验时,一定数量的事件发生的概率。每次的时间。
因此,多项分布是二项分布的推广。
多项分布公式
要计算多项分布概率,必须首先确定数据总数的阶乘与每个事件出现次数的阶乘之间的商,并将结果乘以每个事件的概率的乘积。得出所述事件发生的次数。
换句话说,多项分布的公式如下:

金子:
-
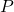
是计算的多项分布的概率。
-

是执行的测试总数。
-

是事件发生的次数

。
-

是事件发生的概率

。
👉您可以使用下面的计算器来计算变量服从多项分布的概率。
多项分布示例
为了完成对多项分布概念的理解,下面您已经解决了计算多项分布概率的示例。
- 一家商店出售三种不同的产品。当顾客购买产品时,购买产品A、产品B或产品C的概率分别为30%、15%和55%。求当商店售出 8 件商品时,其中 2 件是产品 A、1 件是产品 B、5 件是产品 C 的概率。
定义的问题受多项分布支配,因此有必要应用此类概率分布的公式:
![]()
因此我们将问题中的数据代入公式并进行概率计算:
![]()
所以问题陈述中所说的发生的概率是 11.4%。
多项分布计算器
在第一个框中写下每个事件发生的次数,并以相同的顺序在第二个框中写下每个事件发生的概率。然后在最后一个空格中输入尝试的总次数。
数据必须用空格分隔,并使用句点作为小数点分隔符输入。
多项分布的性质
多项式分布具有以下特点:
- 在多项分布中,运行n 次试验时事件i发生的次数的期望值等于执行的试验总数乘以事件发生的概率。
![]()
- 在多项分布中,事件i的方差使用以下表达式计算:
![]()
- 同样,两个事件之间的协方差等于试验总数乘以每个事件的概率的乘积再乘以-1:
![]()
- 多项分布的矩生成函数为: