多项式回归

经过本杰明·安德森博 8月 2, 2023 统计数据 0 条评论

本文解释了统计学中的多项式回归是什么以及它是如何执行的。此外，您将能够看到执行多项式回归的示例。

什么是多项式回归？

多项式回归或多项式回归是一种回归模型，其中使用多项式对自变量 X 和因变量 Y 之间的关系进行建模。

例如，二次多项式回归模型的方程为 y=β ₀ +β ₁ x+β ₂ x ² +ε。

多项式回归对于拟合图形为多项式曲线的数据集非常有用。因此，如果数据样本的点图具有抛物线形状，那么构建二次回归模型会比构建线性回归模型更好。这样，回归模型方程将更好地拟合数据样本。

请注意，多项式回归是非线性回归的一种，就像指数回归和对数回归一样。

多项式回归公式

多项式回归模型的方程为 y=β ₀ +β ₁ x+β ₂ x ² +β ₃ x ³ …+β _m x ^m +ε。

$y=\beta_0+\beta_1 x+\beta_2 x^2+\beta_3 x^3+\dots+\beta_m x^m+\varepsilon$

金子：

$y$

是因变量。
$x$

是自变量。
$\beta_0$

是多项式回归方程的常数。
$\beta_i$

是与变量相关的回归系数

$x^i$

。
$\bm{\varepsilon}$

这是误差或残差，即观测值与模型估计值之间的差异。

所以如果我们有一个样本总共

$n$

观察，我们可以提出矩阵形式的多项式回归模型：

$\begin{pmatrix}y_1\\y_2\\y_3\\\vdots\\y_n\end{pmatrix}=\begin{pmatrix}1&x_1&x_1^2&\dots&x_1^m\\1&x_2&x_2^2&\dots&x_2^m\\1&x_3&x_3^2&\dots&x_3^m\\ \vdots&\vdots&\ddots&\vdots\\1&x_{n}&x_n^2&\dots&x_n^m\end{pmatrix}\cdot\begin{pmatrix}\beta_0\\\beta_1\\\beta_2\\\vdots\\\beta_m\end{pmatrix}+\begin{pmatrix}\varepsilon_1\\\varepsilon_2\\\varepsilon_3\\\vdots\\\varepsilon_n\end{pmatrix}$

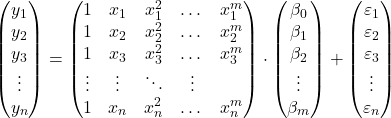
上面的矩阵表达式可以通过为每个矩阵分配一个字母来重写：

$Y=X\beta+\varepsilon$

因此，通过应用最小二乘准则，我们可以得出估计多项式回归模型系数的公式：

$\widehat{\beta}=\left(X^tX\right)^{-1}X^tY$

然而，手动进行这些计算非常费力且耗时，因此使用计算机软件（如 Minitab 或 Excel）更方便，它可以让您更快地执行多项式回归模型。

多项式回归模型示例

现在我们知道了多项式回归的定义及其执行方式，让我们看一个现实生活中的示例来完全理解这个概念。

首先，应该记住，当数据图具有多项式曲线的形状时，应该执行多项式回归模型。例如，如果点图是三次曲线的形式，我们需要构建三次多项式回归模型。

因此，如下图所示，我们的数据点图具有二次形状，因为当我们增加自变量的值时，因变量增长得更快。在这种情况下，执行了线性回归模型，正如您所看到的，它不能很好地拟合这些点，因为它有一些部分，其中线位于所有点的下方，而其中的部分则线位于所有点的上方。

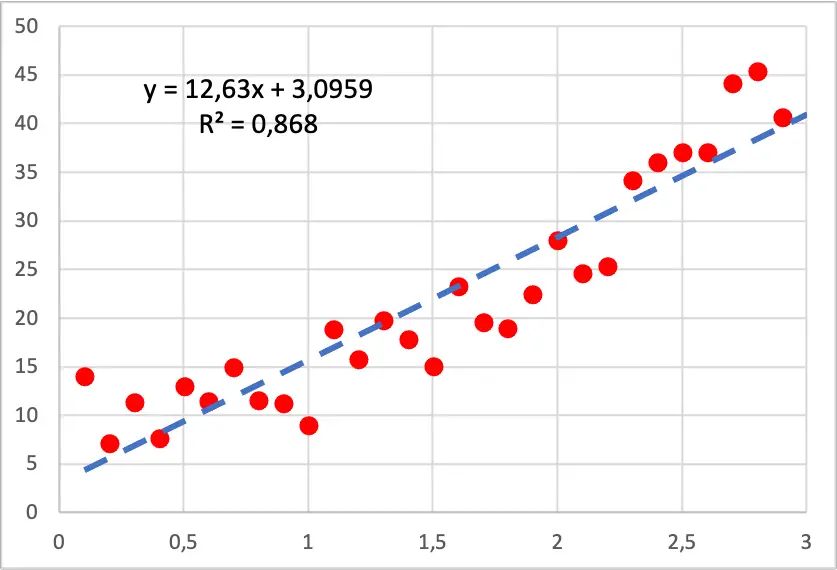
另一方面，如果我们运行二次多项式回归模型，它会更好地拟合样本数据，如下图所示。

多项式回归示例

此外，在开发多项式回归模型时，确定系数显着提高，从 86.80% 提高到 94.05%。因此，新的回归模型可以更好地解释数据集。

另一方面，我们需要执行多项式回归的另一个迹象是残差的绘制。如果在线性回归中，残差图具有抛物线或其他类型多项式的形状，则多项式回归模型肯定更适合所研究的数据。

其他类型的非线性回归

非线性回归主要有三种类型：

多项式回归——回归模型方程采用多项式形式。
对数回归：取自变量的对数。
指数回归：自变量可在方程的指数中找到。

➤请参阅：对数回归
➤请参阅：指数回归

关于作者

本杰明·安德森博

大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多

添加评论