大数定律：定义 + 示例

大数定律指出，随着样本数量的增加， 样本均值越来越接近期望值。

最基本的例子是抛硬币。每次我们抛硬币时，正面朝上的概率是 1/2。因此，在无限次抛掷中出现正面的预期比例是 1/2 或0.5 。

然而，如果我们抛硬币 10 次，我们可能会发现只有 3 次正面朝上。由于 10 次翻转是一个小样本量，因此不能保证头部比例会接近0.5 。

如果我们继续抛硬币 10 次，我们可能会发现 20 次中有 9 次正面朝上。如果我们再抛 10 次，我们可能会发现 30 次中有 22 次正面朝上。

当我们抛硬币时，正面朝上的次数比例将收敛到预期比例0.5 。

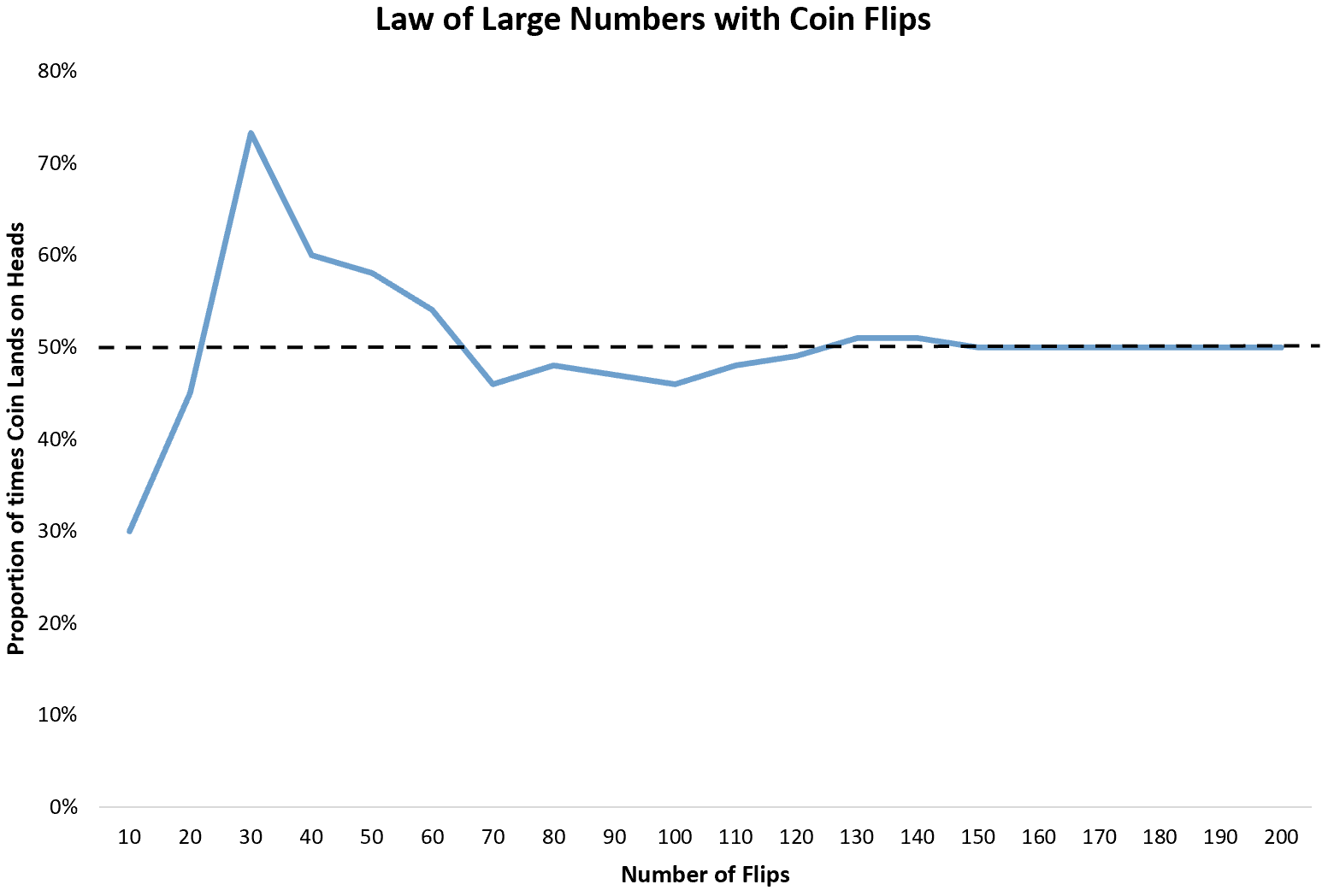
大数定律这个简单的想法被现实生活中许多类型的企业和行业所应用。

赌场中的大数法则

赌场依靠大数定律来可靠地产生利润。对于大多数游戏，赌场获胜的几率约为 51-55%。这意味着个人可以时不时地走运并赢得可观的金额，但在数以万计的个人玩家中，赌场将赢得预期的 51-55% 的机会。

例如，杰西卡可以在赌场玩几局游戏并赢得 50 美元。

迈克也可能玩几场比赛并损失 70 美元。

约翰可以玩几场比赛并赢得 25 美元。

苏珊可能会玩几局游戏并输掉 40 美元。

有些玩家会赢钱，有些玩家会输钱，但由于游戏的设计方式，赌场可以确保他们从成千上万的玩家中获胜。

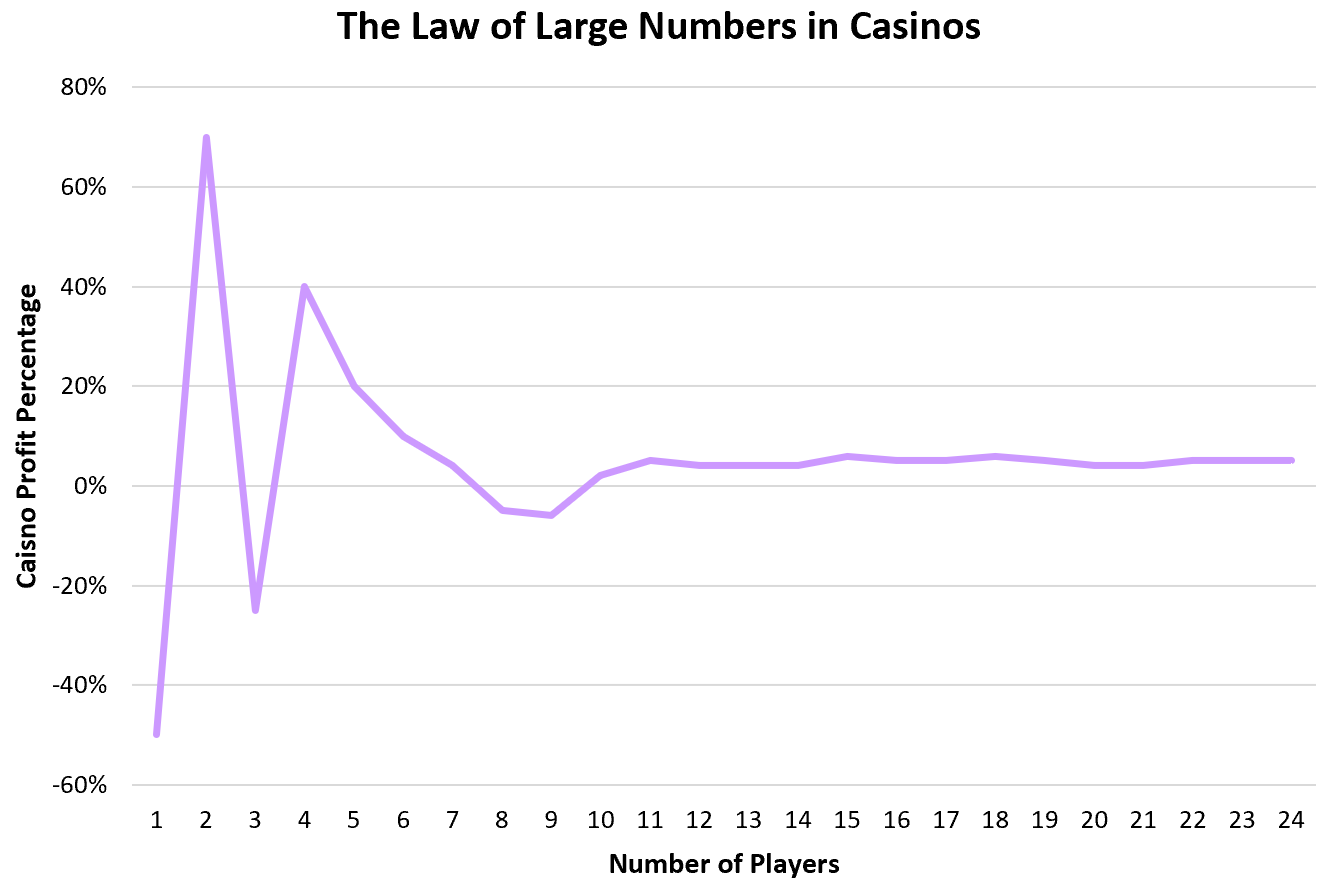
保险中的大数法则

保险公司也依靠大数法则来保持盈利。

其基本理念是，成千上万的保险公司可以为每月支付一定保费的人提供保险，而他们的受保人中只有一小部分实际上需要使用保险来支付重大的意外费用。

例如，1,000 人每人每年可以支付 1,000 美元的保险费，这将为保险公司带来 1,000,000 美元的利润。

然而，90人可能每人需要从保险公司收到10,000美元，以支付与各种事故相关的意外费用，从而导致保险公司损失900,000美元。

最终，保险公司获利$1,000,000 – $900,000 = $100,000 。

这意味着保险公司平均可以为数千人赚取相当可预测的利润。

请注意，这种经济模式之所以有效，是因为保险公司为大量人员提供保险。如果他们只为 10 人投保，那就风险太大了，因为巨额的意外费用可能会毁掉整个业务。

因此，保险公司依靠大数定律以可预测的方式预测其利润。

可再生能源中的大数定律

可再生能源公司也使用大数定律。

基本思想是风力涡轮机和太阳能电池板可以为发电机提供电力，为不同的业务部门提供电力。然而，外面没有风或阳光，这意味着风力涡轮机和太阳能电池板并不总是能够为发电机提供可靠的电力。

可再生能源公司解决这个问题的方法是将数以万计的风力涡轮机或太阳能电池板连接到一个电网，从而使这些能源更有可能产生可靠的能源。为网络提供能源。

预测这些电源将产生多少能量也更容易，因为工程师可以简单地获取数万个风力涡轮机或太阳能电池板的预期平均值。

关于这一现象的详细解释可以在这篇《科学美国人》的文章中找到。