如何使用 z 表（附示例）

z 表是告诉您标准正态分布中低于某个 z 分数的值的百分比的表。

z 分数只是告诉您单个数据值与平均值的标准差有多少。计算方法如下：

z 分数 = (x – μ) / σ

金子：

• x：单个数据值
• μ：总体平均值
• σ：总体标准差

本教程展示了使用 z 表的几个示例。

实施例1

某次高考成绩呈正态分布，平均值μ = 82，标准差 σ = 8。考试成绩低于 84 分的学生大约占多少比例？

第 1 步：找到 z 分数。

首先，我们将找到与考试分数 84 相关的 z 分数：

z 分数 = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0.25

步骤 2：使用 z 图表查找与 z 分数对应的百分比。

接下来，我们将在 z 表中查找值0.25 ：

大约59.87%的学生在这次考试中得分低于84分。

实施例2

某个花园中植物的高度呈正态分布，平均值为 μ = 26.5 英寸，标准差为 σ = 2.5 英寸。大约有多少植物的高度超过 26 英寸？

第 1 步：找到 z 分数。

首先，我们将找到与 26 英寸高度相关的 z 分数。

z 分数 = (x – μ) / σ = (26 – 26.5) / 2.5 = -0.5 / 2.5 = -0.2

步骤 2：使用 z 图表查找与 z 分数对应的百分比。

接下来我们将寻找值-0.2  在表z中：

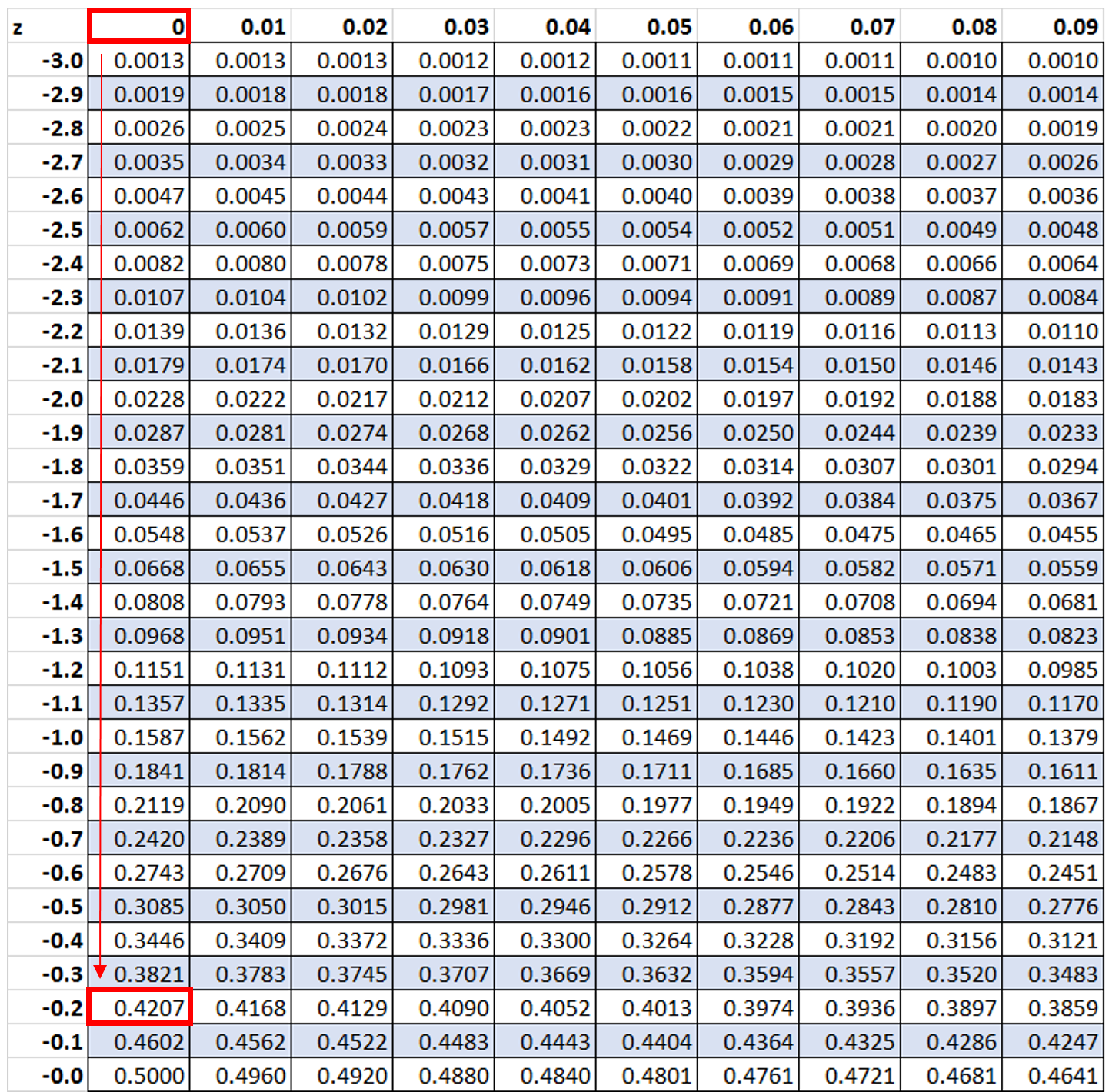
我们看到 42.07% 的值低于 -0.2 的 z 分数。然而，在这个例子中，我们想知道大于-0.2的值的百分比，我们可以使用公式100% – 42.07% = 57.93%找到。

因此，这个花园中大约59.87%的植物高度超过 26 英寸。

实施例3

某种海豚的体重呈正态分布，平均值为 μ = 400 磅，标准差为 σ = 25 磅。体重在 410 到 425 磅之间的海豚大约占多少百分比？

第 1 步：找到 z 分数。

首先，我们将找到与 410 本书和 425 本书相关的 z 分数

z 分数 410 = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0.4

z 分数 425 = (x – μ) / σ = (425 – 400) / 25 = 25 / 25 = 1

步骤 2：使用 z 图表查找与每个 z 分数对应的百分比。

首先，我们将寻找值0.4  在表z中：

接下来我们将寻找值1  在表z中：

最后，我们将从最大值减去最小值： 0.8413 – 0.6554 = 0.1859 。

因此，大约18.59%的海豚体重在 410 至 425 磅之间。

其他资源

正态分布简介
正态分布面积计算器
Z 分数计算器