如何解释残差标准误差

残差标准误差用于衡量回归模型对数据集的拟合程度。

简而言之，它测量回归模型中残差的标准差。

计算方法如下：

残差标准误差 = √ Σ(y – ŷ) ² /df

金子：

• y：观测值
• ŷ：预测值
• df：自由度，计算为观察总数 – 模型参数总数。

残差标准误差越小，回归模型对数据集的拟合效果越好。相反，残差标准误差越高，回归模型对数据集的拟合程度就越差。

具有较小残差标准误差的回归模型的数据点将紧密聚集在拟合回归线周围：

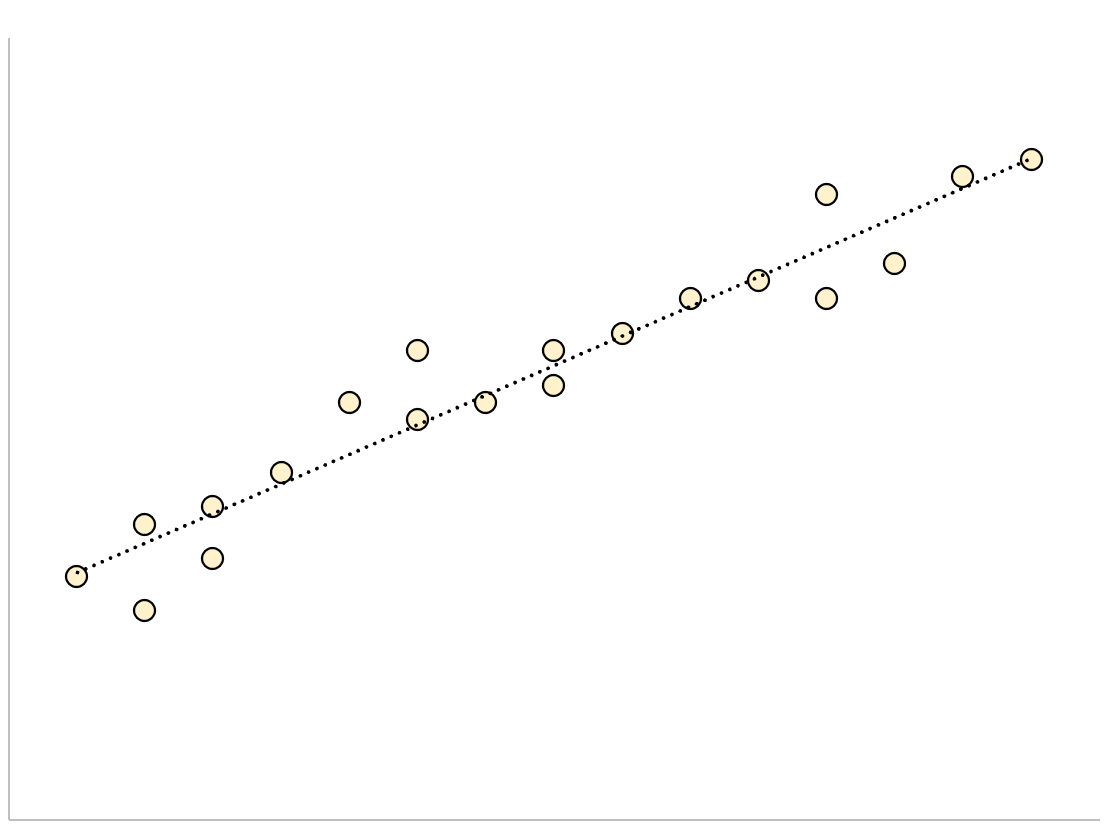
该模型的残差（观测值与预测值之间的差异）会很小，意味着残差标准误差也会很小。

相反，具有较大残差标准误差的回归模型的数据点将更加松散地分散在拟合回归线周围：

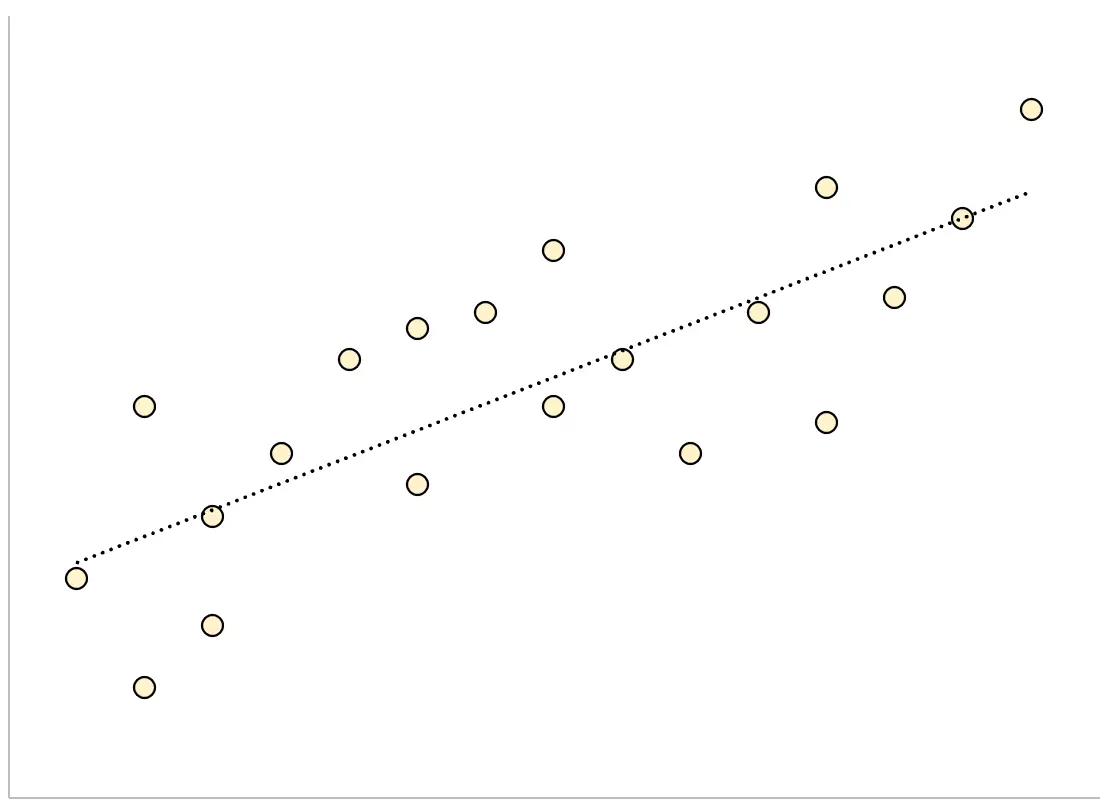
该模型的残差会更大，这意味着残差标准误差也会更大。

以下示例演示如何计算和解释 R 中回归模型的残差标准误差。

示例：解释残差标准误差

假设我们要拟合以下多元线性回归模型：

mpg = β ₀ + β ₁ (排量) + β ₂ (功率)

该模型使用预测变量“排量”和“马力”来预测给定汽车每加仑行驶的英里数。

以下代码显示了如何在 R 中拟合此回归模型：

 #load built-in mtcars dataset
data(mtcars)

#fit regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Call:
lm(formula = mpg ~ disp + hp, data = mtcars)

Residuals:
    Min 1Q Median 3Q Max 
-4.7945 -2.3036 -0.8246 1.8582 6.9363 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

在结果的底部，我们可以看到该模型的剩余标准误差为3.127 。

这告诉我们，回归模型预测汽车 mpg 的平均误差约为 3,127。

使用残差标准误差来比较模型

残差标准误差对于比较不同回归模型的拟合特别有用。

例如，假设我们拟合两个不同的回归模型来预测汽车每加仑英里数。各模型的残差标准误如下：

• 模型1的残差标准误差： 3.127
• 模型2的残差标准误差： 5.657

由于模型 1 的残差标准误差较低，因此它比模型 2 更适合数据。因此，我们更愿意使用模型 1 来预测汽车 mpg，因为它所做的预测更接近观察到的汽车 mpg 值。

其他资源

如何在 R 中执行简单线性回归
如何在 R 中执行多元线性回归
如何在 R 中创建残差图