如何读取相关矩阵

在统计学中，我们经常寻求理解两个变量之间的关系。

例如，我们可能想了解学生学习的小时数与考试成绩之间的关系。

量化这种关系的一种方法是使用Pearson 相关系数，它是两个变量之间线性关联的度量。它的值介于 -1 和 1 之间，其中：

• -1 表示两个变量之间完全负线性相关
• 0 表示两个变量之间不存在线性相关
• 1 表示两个变量之间存在完全正线性相关

相关系数离零越远，两个变量之间的相关性越强。

相关：什么被认为是“强”相关性？

但在某些情况下，我们想要了解多对变量之间的相关性。在这些情况下，我们可以创建一个相关矩阵，它是一个方表，显示多个变量之间的相关系数。

相关矩阵示例

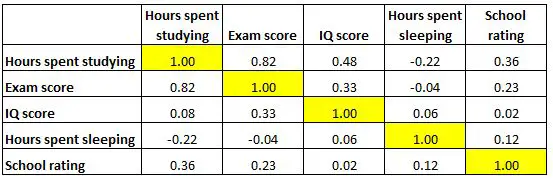
下面的相关矩阵显示了几个与教育相关的变量之间的相关系数：

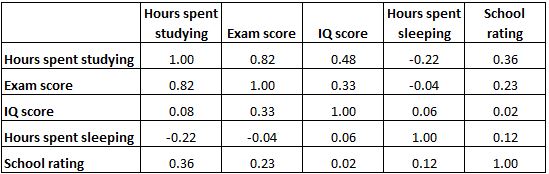
表中的每个单元格显示两个特定变量之间的相关性。例如，下面突出显示的单元格显示“学习时间”和“考试成绩”之间的相关性为0.82 ，表明它们呈强正相关。学习时间越长与考试成绩越高密切相关。

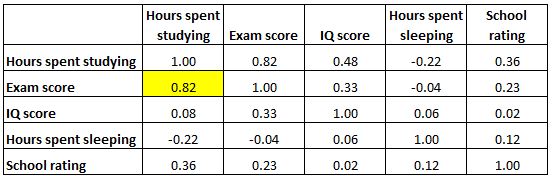
下面突出显示的单元格显示“学习时间”和“睡眠时间”之间的相关性为-0.22 ，表明它们呈弱负相关。学习时间越长，睡眠时间越少。

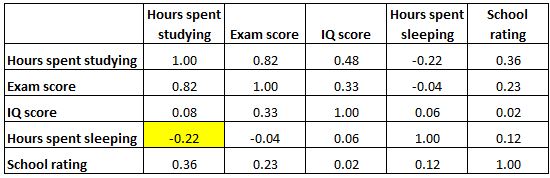
下面突出显示的单元格显示“睡眠时间”和“IQ 分数”之间的相关性为0.06 ，表明它们基本上不相关。学生的睡眠时间和他们的智商分数之间几乎没有关联。

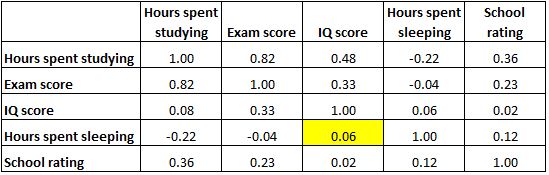
另请注意，表格对角线上的相关系数均等于 1，因为每个变量与其自身完全相关。这些细胞对于解释没有用处。

相关矩阵的变体

请注意，相关矩阵是完全对称的。例如，右上角的单元格显示与左下角单元格完全相同的值：

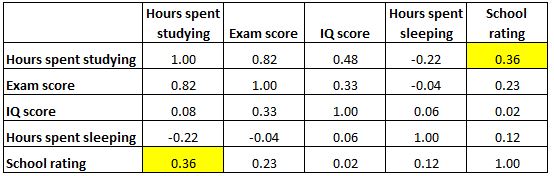
事实上，这两个单元测量了“学习时间”和“学校成绩”之间的相关性。

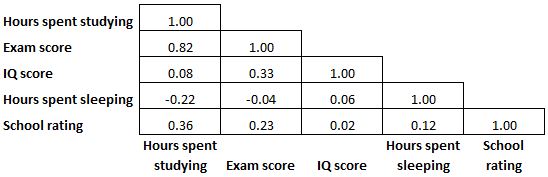
因为相关矩阵是对称的，所以矩阵中显示的相关系数有一半是多余的、不必要的。因此，有时只会显示一半的相关矩阵：

有时相关矩阵会像热图一样着色，以使相关系数更容易阅读：

何时使用相关矩阵

在实践中，常用相关矩阵有以下三个原因：

1. 相关矩阵可以方便地总结一组数据。

相关矩阵是总结数据集中所有变量之间相关性的简单方法。例如，假设我们有以下数据集，其中包含 1,000 名学生的以下信息：

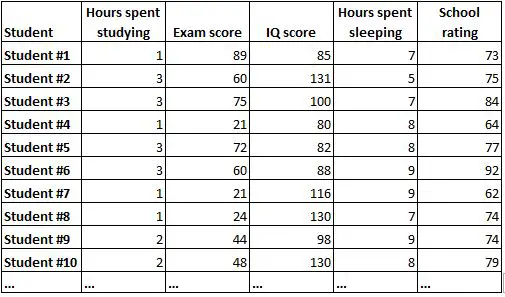
仅通过查看原始数据很难理解每个变量之间的关系。幸运的是，相关矩阵可以帮助我们快速了解每对变量之间的相关性。

2. 相关矩阵用作回归的诊断。

多元线性回归的关键假设之一是模型中没有自变量与模型中的任何其他变量强相关。

当两个自变量高度相关时，会导致称为多重共线性的问题，并使回归结果难以解释。

发现潜在多重共线性问题的最简单方法之一是查看相关矩阵并目视检查是否有任何变量彼此高度相关。

3. 相关矩阵可以用作其他分析的输入。

相关矩阵用作其他复杂分析的输入，例如探索性因素分析和结构方程模型。

其他资源

以下教程解释了如何使用各种统计软件创建相关矩阵：

如何在 Excel 中创建相关矩阵
如何在 SPSS 中创建相关矩阵
如何在 Stata 中创建相关矩阵
如何在 Python 中创建相关矩阵