如何通过 t 检验手动计算 p 值

统计学中最常用的检验之一是t 检验，它通常用于确定总体平均值是否等于某个值。

例如，假设我们想知道某种植物物种的平均高度是否等于 15 英寸。为了测试这一点，我们可以收集 20 株植物的随机样本，找到样本均值和样本标准差，并执行 t 检验以确定平均高度是否实际上为 15 英寸。

检验的原假设和备择假设如下：

H ₀ : µ = 15

H _a : µ ≠ 15

检验统计量的公式为：

t = ( X -μ) / (s/ √n )

其中x是样本平均值， μ是假设平均值（在我们的示例中为 15）， s是样本标准差， n是样本大小。

一旦我们知道了t的值，我们就可以使用统计软件或在线计算器来找到相应的 p 值。如果 p 值低于某个 alpha 水平（常见选择为 0.01、0.05 和 0.10），那么我们可以拒绝零假设并得出平均植物高度不等于 15 英寸的结论。

但是，也可以使用 t 分布表手动估计检验 p 值。在本文中，我们将解释如何执行此操作。

示例：根据 t 检验手动计算 p 值

问题：Bob 想知道某种植物的平均高度是否等于 15 英寸。为了测试这一点，他随机收集了 20 株植物的样本，发现样本平均值为 14 英寸，样本标准差为 3 英寸。使用 0.05 的 alpha 水平执行 t 检验，以确定真实的平均人口身高是否实际上为 15 英寸。

解决方案：

步骤 1：陈述原假设和备择假设。

H ₀ : µ = 15

H _a : µ ≠ 15

步骤 2：求检验统计量。

t = ( x -μ) / (s/ √n ) = (14-15) / (3/ √20 ) = -1.49

步骤 3：查找检验统计量的 p 值。

要手动查找 p 值，我们需要使用具有 n-1 自由度的 t 分布表。在我们的示例中，样本大小为 n = 20，因此 n-1 = 19。

在下面的 t 分布表中，我们需要查看左侧与“19”对应的行，并尝试找到检验统计量1.49的绝对值。

请注意，1.49 并未出现在表中，但它落在1.328和1.729两个值之间。

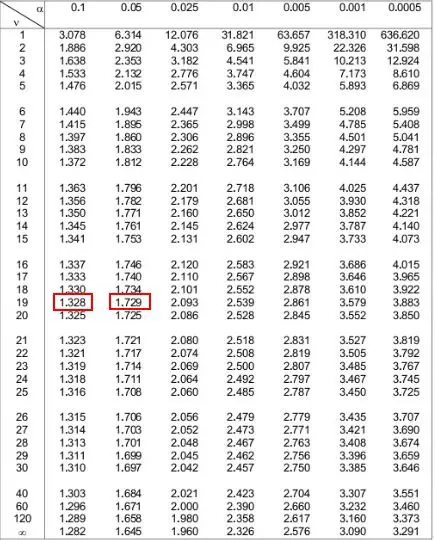
然后我们可以查看表格顶部与这两个数字对应的两个 alpha 级别。我们看到它们是0.1和0.05 。

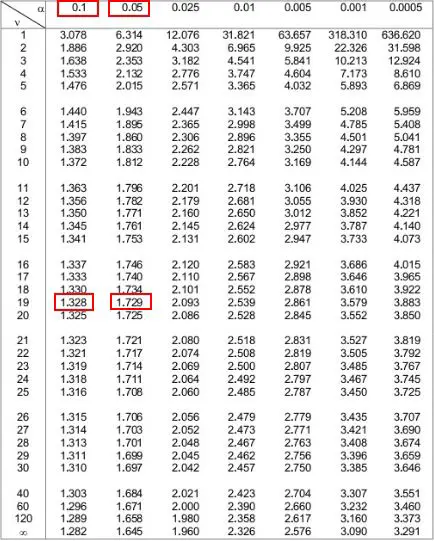
这意味着单尾检验的 p 值介于 0.1 和 0.05 之间。我们称之为 0.075。由于我们的 t 检验是双尾的，因此我们需要将该值乘以 2。因此，我们的估计 p 值为 0.075 * 2 = 0.15 。

第四步：得出结论。

由于该 p 值不低于所选的 alpha 水平 0.05，因此我们不能拒绝原假设。因此，我们没有足够的证据表明该植物物种的真实平均高度不是 15 英寸。

用计算器检查结果

我们可以将t检验统计量和自由度插入在线 p 值计算器，以查看我们估计的 p 值与真实 p 值的接近程度：

真实的 p 值为0.15264 ，这非常接近我们估计的 p 值0.15 。

结论

我们在本文中看到，可以使用 t 分布表手动估计 t 检验的 p 值。但是，在大多数情况下，您永远不需要手动计算 p 值，您可以使用 R 和 Excel 等统计软件或在线计算器来查找检验的准确 p 值。

在大多数情况下，尤其是在严格的统计研究和实验中，您需要使用计算器从 t 检验中找到尽可能精确的精确 p 值，但很高兴知道您始终可以手动估计如果确实需要的话，可以使用 t 检验的 p 值。