Ancova（方差分析）简介

ANCOVA代表“协方差分析”。要了解方差分析的工作原理，首先了解方差分析会有所帮助。

方差分析  （方差分析）用于确定三个或更多独立组的平均值之间是否存在统计显着差异。

例如，假设我们想知道学习技巧是否会影响某个班级学生的考试成绩。我们把全班随机分成三组。每个小组在一个月内使用不同的学习技巧来准备考试。月底，所有学生参加相同的考试。

为了查明学习技巧是否对考试成绩有影响，我们可以进行单向方差分析，这将告诉我们三组的平均分数之间是否存在统计上的显着差异。

ANCOVA是 ANOVA 的扩展，其中我们想要确定在考虑一个或多个协变量后，三个或更多独立组之间是否存在统计显着差异。

协变量是随响应变量变化的连续变量。

例如，假设我们想知道学习技巧是否对考试成绩有影响，但我们想考虑学生在课堂上已有的成绩。我们可以使用他们当前的成绩作为协变量，并执行 ANCOVA 来确定三组的平均考试成绩之间是否存在统计上的显着差异。

这使我们能够测试一旦协变量的影响被消除，学习技术是否会对考试成绩产生影响。

因此，如果我们发现三种学习技巧之间的考试成绩存在统计上的显着差异，那么即使考虑到学生当前在班级中的成绩（c’也就是说，如果他们已经做得很好或者如果他们已经做得很好）。不在课堂上） 。

方差分析假设

在执行 ANCOVA 之前，确保满足以下假设非常重要：

• 协变量和因子变量是独立的——协变量和因子变量必须彼此独立，因为只有当协变量和因子变量独立作用于模型时，在模型中添加协变量项才有意义。响应变量。
• 协变量是连续数据。协变量必须是连续的（即区间或比率数据）。
• 方差同质性——组间方差应大致相等。
• 独立性——每组的观察结果必须是独立的。
• 正态性——每组数据应大致呈正态分布。
• 没有极端异常值– 任何组中都不应该存在可能显着影响 ANCOVA 结果的极端异常值。

协方差分析：示例

一位老师想知道三种不同的学习技巧是否会影响考试成绩，但她想考虑到学生当前在班上的成绩。

它将使用以下变量执行 ANCOVA：

• 因素变量：技术研究
• 协变量：当前分数
• 响应变量：考试成绩

下表列出了招募参与该研究的 15 名学生的数据集：

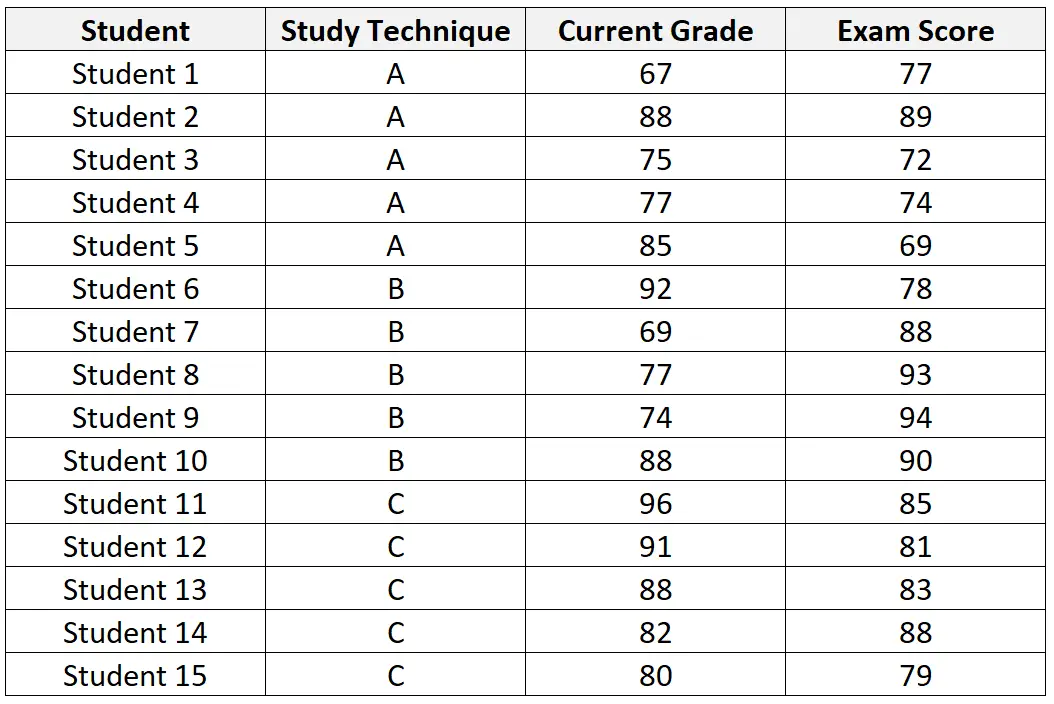
对数据集执行 ANCOVA 后，教师获得以下结果：

研究技术的 p 值为0.03155 。由于该值小于 0.05，因此我们可以拒绝原假设，即即使考虑了学生在班级中的当前成绩，每种学习技术都会导致相同的平均考试成绩。

为了准确确定哪些学习技巧会产生不同的平均考试成绩，教师需要进行事后测试。

其他资源

如何在 Excel 中执行 ANCOVA
如何在 R 中执行 ANCOVA
如何在 Python 中执行 ANCOVA
ANOVA、ANCOVA、MANOVA 和 MANCOVA 之间的区别