什么是完美多重共线性？ （定义和示例）

在统计学中，当两个或多个预测变量彼此高度相关，以致它们在回归模型中不提供唯一或独立的信息时，就会出现多重共线性。

如果变量之间的相关程度足够高，则在拟合和解释回归模型时可能会出现问题。

多重共线性最极端的情况称为完全多重共线性。当两个或多个预测变量彼此具有精确的线性关系时，就会发生这种情况。

例如，假设我们有以下数据集：

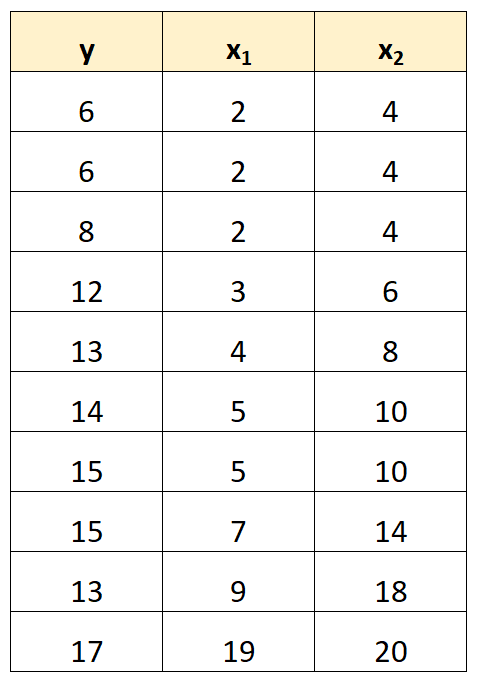
请注意，预测变量 x ₂的值只是 x ₁乘以 2 的值。

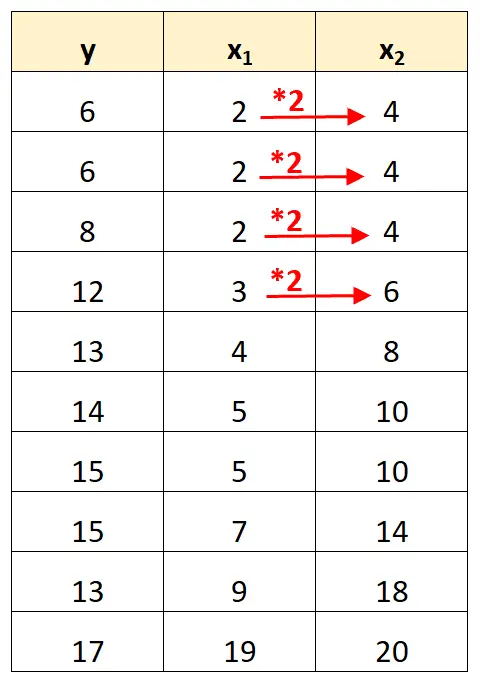
这是完美多重共线性的一个例子。

完美多重共线性问题

当数据集中存在完美多重共线性时，普通最小二乘法无法产生回归系数的估计。

事实上，在保持另一个预测变量 (x ₂ ) 恒定的同时，不可能估计预测变量 (x ₁ ) 对响应变量 (y) 的边际效应，因为 x ₂总是在 x ₁移动时精确移动。

简而言之，完美的多重共线性使得无法估计回归模型中每个系数的值。

如何处理完美多重共线性

处理完美多重共线性的最简单方法是删除与另一个变量具有精确线性关系的一个变量。

例如，在我们之前的数据集中，我们可以简单地删除 x ₂作为预测变量。

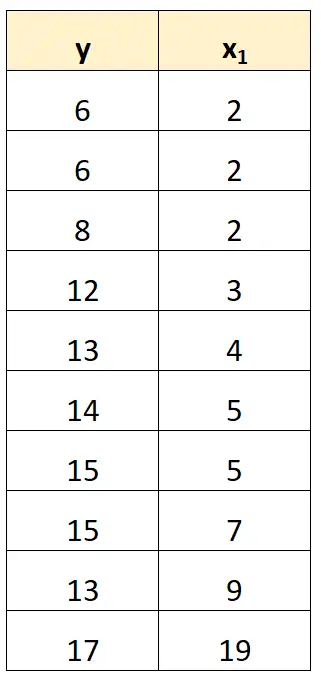
然后，我们将使用 x ₁作为预测变量，y 作为响应变量来拟合回归模型。

完美多重共线性的示例

以下示例显示了实践中完美多重共线性的三种最常见情况。

1. 预测变量是另一个变量的倍数

假设我们想使用“身高（厘米）”和“身高（米）”来预测某种海豚的体重。

我们的数据集可能如下所示：

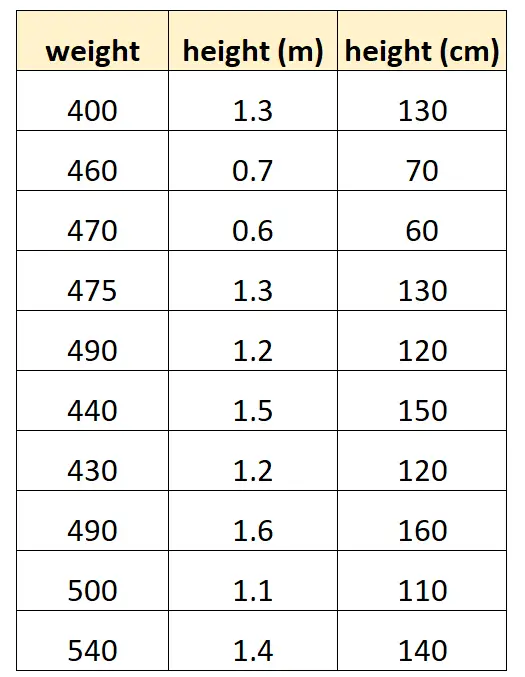
请注意，“以厘米为单位的身高”的值仅等于“以米为单位的身高”乘以 100。这是完美多重共线性的情况。

如果我们尝试使用此数据集在 R 中拟合多元线性回归模型，我们将无法生成预测变量“米”的系数估计：

 #define data
df <- data. frame (weight=c(400, 460, 470, 475, 490, 440, 430, 490, 500, 540),
                 m=c(1.3, .7, .6, 1.3, 1.2, 1.5, 1.2, 1.6, 1.1, 1.4),
                 cm=c(130, 70, 60, 130, 120, 150, 120, 160, 110, 140))

#fit multiple linear regression model
model <- lm(weight~m+cm, data=df)

#view summary of model
summary(model)

Call:
lm(formula = weight ~ m + cm, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-70,501 -25,501 5,183 19,499 68,590 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 458,676 53,403 8,589 2.61e-05 ***
m 9.096 43.473 0.209 0.839    
cm NA NA NA NA    
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 41.9 on 8 degrees of freedom
Multiple R-squared: 0.005442, Adjusted R-squared: -0.1189 
F-statistic: 0.04378 on 1 and 8 DF, p-value: 0.8395

2. 预测变量是另一个变量的变换版本

假设我们想使用“分数”和“缩放分数”来预测篮球运动员的评分。

假设变量“缩放点”计算如下：

缩放点 = ( 点 – μ_点) / σ_点

我们的数据集可能如下所示：

请注意，每个“缩放点”值只是“点”的标准化版本。这是完全多重共线性的情况。

如果我们尝试使用此数据集在 R 中拟合多元线性回归模型，我们将无法生成“缩放点”预测变量的系数估计：

 #define data
df <- data. frame (rating=c(88, 83, 90, 94, 96, 78, 79, 91, 90, 82),
                 pts=c(17, 19, 24, 29, 33, 15, 14, 29, 25, 22))

df$scaled_pts <- (df$pts - mean(df$pts)) / sd(df$pts)

#fit multiple linear regression model
model <- lm(rating~pts+scaled_pts, data=df)

#view summary of model
summary(model)

Call:
lm(formula = rating ~ pts + scaled_pts, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-4.4932 -1.3941 -0.2935 1.3055 5.8412 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 67.4218 3.5896 18.783 6.67e-08 ***
pts 0.8669 0.1527 5.678 0.000466 ***
scaled_pts NA NA NA NA    
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.953 on 8 degrees of freedom
Multiple R-squared: 0.8012, Adjusted R-squared: 0.7763 
F-statistic: 32.23 on 1 and 8 DF, p-value: 0.0004663

3. 虚拟变量陷阱

另一种可能发生完美多重共线性的情况称为虚拟变量陷阱。这是当我们想要在回归模型中获取分类变量并将其转换为具有 0、1、2 等值的“虚拟变量”时。

例如，假设我们要使用预测变量“年龄”和“婚姻状况”来预测收入：

要使用“婚姻状况”作为预测变量，我们必须首先将其转换为虚拟变量。

为此，我们可以将“单身”保留为基值，因为这种情况最常发生，并将值 0 或 1 分配给“已婚”和“离婚”，如下所示：

错误的做法是创建三个新的虚拟变量，如下所示：

在这种情况下，“单身”变量是“已婚”和“离婚”变量的完美线性组合。这是完美多重共线性的一个例子。

如果我们尝试使用此数据集在 R 中拟合多元线性回归模型，我们将无法为每个预测变量生成系数估计：

 #define data
df <- data. frame (income=c(45, 48, 54, 57, 65, 69, 78, 83, 98, 104, 107),
                 age=c(23, 25, 24, 29, 38, 36, 40, 59, 56, 64, 53),
                 single=c(1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0),
                 married=c(0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1),
                 divorced=c(0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0))

#fit multiple linear regression model
model <- lm(income~age+single+married+divorced, data=df)

#view summary of model
summary(model)

Call:
lm(formula = income ~ age + single + married + divorced, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-9.7075 -5.0338 0.0453 3.3904 12.2454 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)   
(Intercept) 16.7559 17.7811 0.942 0.37739   
age 1.4717 0.3544 4.152 0.00428 **
single -2.4797 9.4313 -0.263 0.80018   
married NA NA NA NA   
divorced -8.3974 12.7714 -0.658 0.53187   
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 8.391 on 7 degrees of freedom
Multiple R-squared: 0.9008, Adjusted R-squared: 0.8584 
F-statistic: 21.2 on 3 and 7 DF, p-value: 0.0006865

其他资源

回归中的多重共线性和 VIF 指南
如何在R中计算VIF
如何用Python计算VIF
如何在Excel中计算VIF