对数回归

本文解释什么是对数回归以及它是如何执行的。此外，您可以查看对数回归的示例来充分理解该概念。

什么是对数回归？

对数回归是一种在方程中包含对数的回归模型。具体来说，在对数回归中，取自变量的对数。因此，对数回归模型的方程为 y=a+b·ln(x)。

当样本数据形成对数曲线时，对数回归对于拟合回归模型非常有用，从而使回归模型更好地拟合样本数据。下面我们将了解何时应该执行对数回归。

因此，对数回归是非线性回归的一种，就像指数回归和多项式回归一样。

对数回归公式

对数回归模型涉及取自变量的对数。因此，对数回归方程的公式为y=a+b·ln(x)。

金子：

• 

  是因变量。

• 

  是自变量。

• 

  是回归系数。

注意，y=a+b·ln(x)实际上是一条直线的方程，但它不是指原始变量x和y，而是指变量ln(x)和y。

什么时候进行对数回归？

当样本数据的图形是对数曲线时，即当点的图形类似于对数函数的图形时，我们需要进行对数回归。

看下面的散点图，线性回归模型已拟合到数据集。正如您所看到的，该线并不是数据的糟糕近似值，但是，如果您小心的话，图表开头的值会比结尾处的值增加得更快，因此该线与观察结果并不完全匹配。

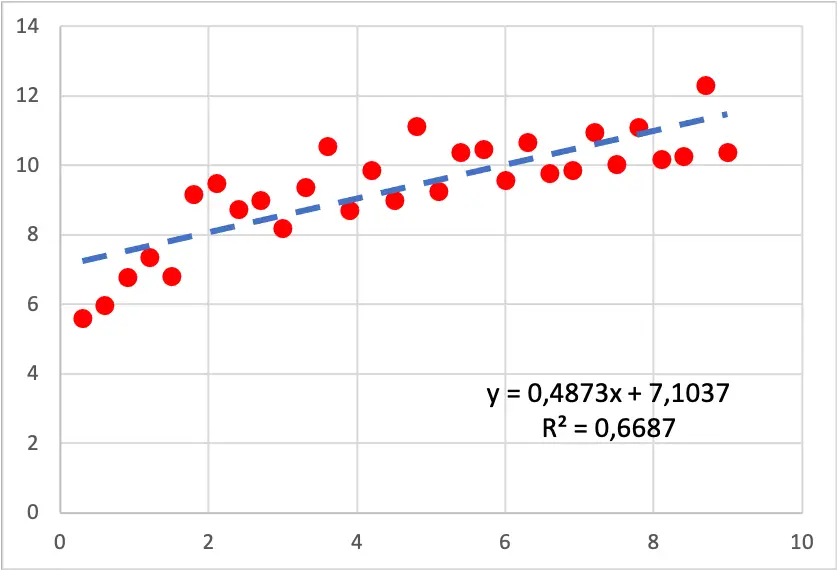
因此，值得尝试创建一个对数回归模型，因为它看起来数据遵循对数曲线。对数回归模型得到的结果如下：

正如您在上图中所看到的，生成的对数回归模型更适合样本数据。事实上，决定系数从 66.87% 增加到 80.05%，因此模型现在可以更好地解释数据样本。因此，在这种情况下，最好使用逻辑回归来找到近似数据值的方程。

其他类型的非线性回归

非线性回归的三种最常见情况是：

• 对数回归：取自变量的对数。
• 指数回归：自变量是方程的指数。
• 多项式回归：回归模型方程采用多项式形式。