对数正态分布

经过本杰明·安德森博 8月 3, 2023 可能性 0 条评论

本文解释了统计学中的对数正态分布是什么。因此，您将了解对数正态分布的属性以及此类概率分布的图形。

什么是对数正态分布？

对数正态分布或对数正态分布是一种概率分布，定义其对数服从正态分布的随机变量。

因此，如果变量 X 服从正态分布，则指数函数 e ^x服从对数正态分布。

$X\sim \text{Lognormal}(\mu,\sigma^2)$

请注意，对数正态分布只能在变量值为正时使用，因为对数是一种仅采用一个正参数的函数。

在对数正态分布在统计中的不同应用中，我们区分使用该分布来分析金融投资和进行可靠性分析。

对数正态分布也称为Tinaut 分布，有时也写为对数正态分布或对数正态分布。

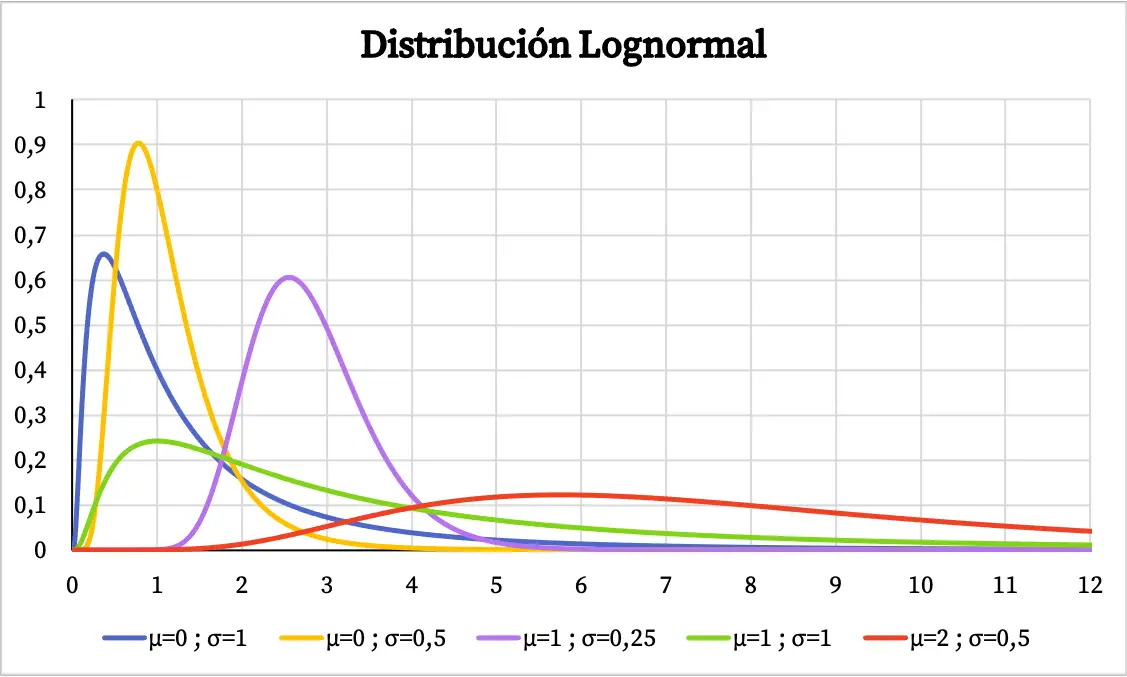
对数正态分布图

现在我们知道了对数正态分布的定义，我们将在本节中看到对数正态分布的图形表示如何根据其算术平均值和标准差的值而变化。

对数正态分布的密度函数图如下：

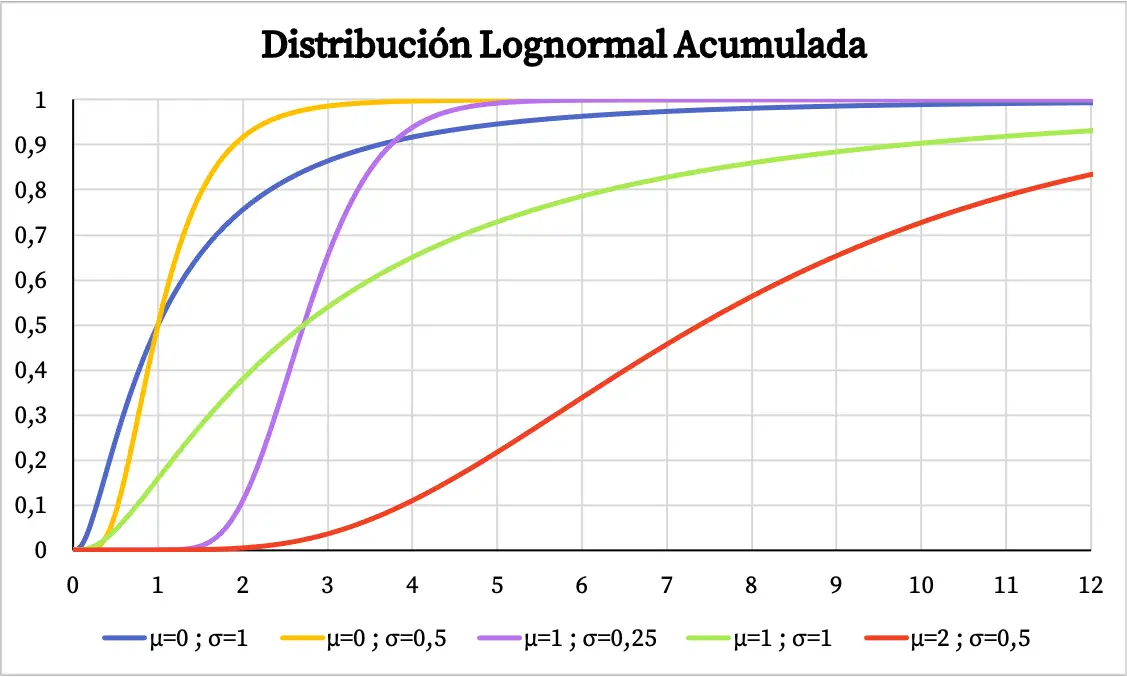
另一方面，对数正态分布的累积概率图如下：

对数正态分布的特征

对数正态分布具有以下特征：

对数正态分布由两个参数的值定义，即算术平均值 μ 和方差 σ ² 。

$X\sim \text{Lognormal}(\mu,\sigma^2)$

对数正态分布的域由正实数组成，因为对数不接受负值或零值。

$x\in (0,+\infty)$

对数正态分布的期望等于平均值加方差之和除以 2 得出的数字 e。

$\displaystyle E[X]=e^{\mu+\frac{\sigma^2}{2}}$

另一方面，对数正态分布的方差可以使用以下表达式计算：

$Var(X)=\left(e^{\sigma^2}-1\right)\cdot e^{2\mu+\sigma^2$

对数正态分布的众数相当于将数字 e 求为分布平均值。

$Mo=e^\mu$

对数正态分布的偏度系数可以通过应用以下公式确定：

$\displaystyle A=\left(e^{\sigma^2}+2\right)\cdot\sqrt{e^{\sigma^2}-1}$

对数正态分布的密度函数的公式为：

$\displaystyle P[X=x]=\frac{1}{\sigma \cdot x\cdot \sqrt{2 \pi}}\cdot \exp\left(-\frac{(\ln x-\mu)^2}{2\sigma^2}\right)$

对数正态分布的累积概率函数的公式为：

$\displaystyle P[X\leq x]=\Phi\left(\frac{\ln x-\mu}{\sigma}\right)$

金子

$\Phi$

是标准正态分布的累积概率函数。

对数正态分布的算术平均值大于中值。

$\mu > Me” title=”Rendered by QuickLaTeX.com” height=”16″ width=”61″ style=”vertical-align: -4px;”></p></p> </div>  <div class=$

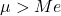
关于作者

本杰明·安德森博

大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多

什么是对数正态分布？

对数正态分布图

对数正态分布的特征

关于作者

本杰明·安德森博

添加评论