对称分布：定义+示例

在统计学中，对称分布是左侧和右侧彼此镜像的分布。

最著名的对称分布是正态分布，它具有明显的钟形形状。

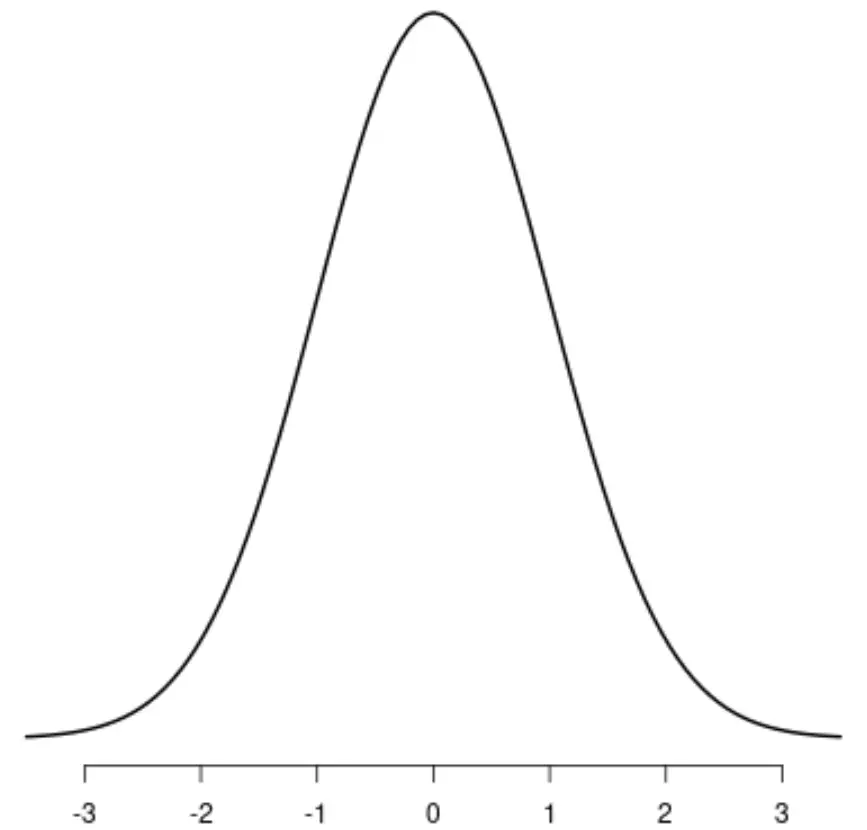
如果你要在分布的中心画一条线，分布的左侧和右侧将完美地相互镜像：

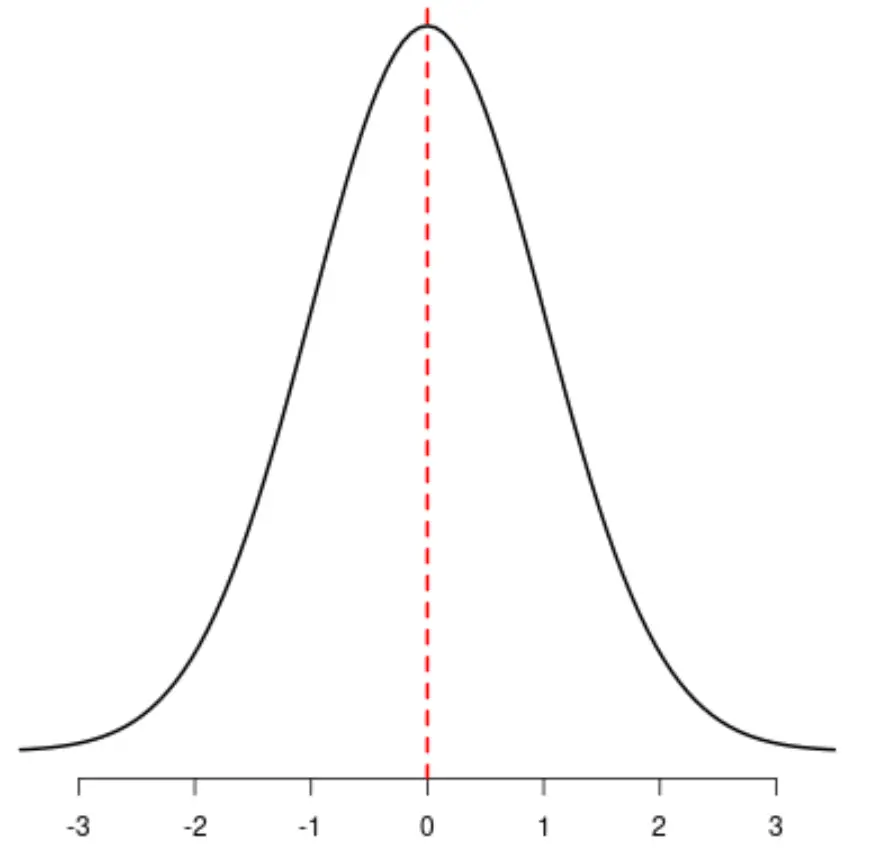
在统计学中，偏度是描述分布对称性的一种方式。该值可以是负数、零或正数。

对于对称分布，不对称性为零。

这与具有负偏度的左偏分布形成对比：

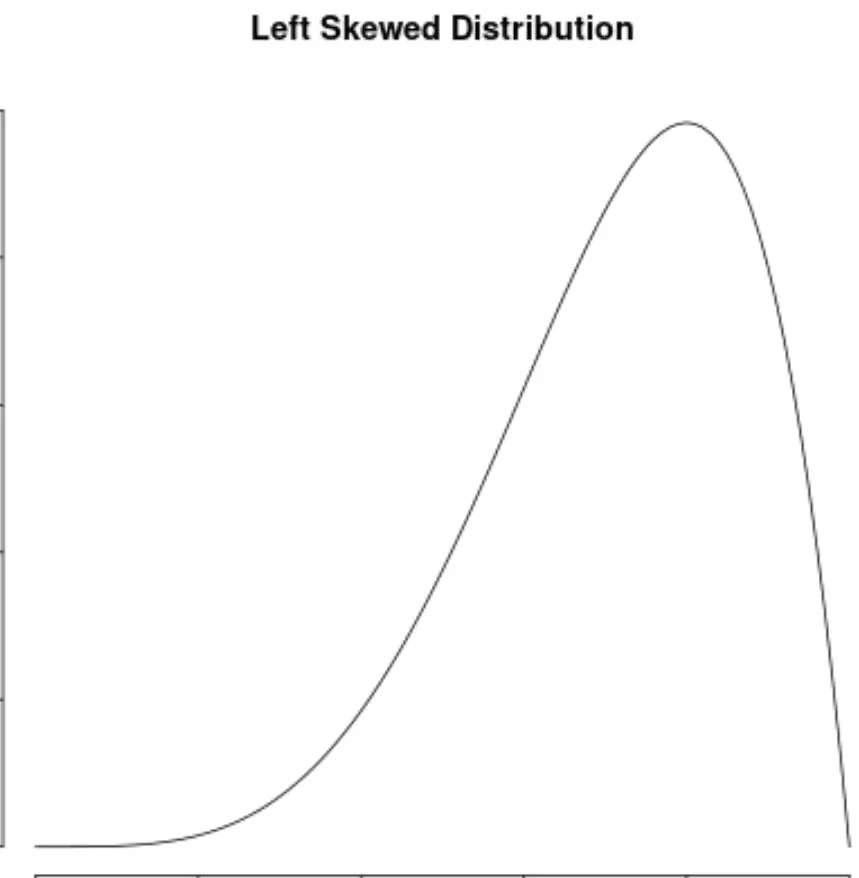
这也与具有正偏度的右偏分布形成对比：

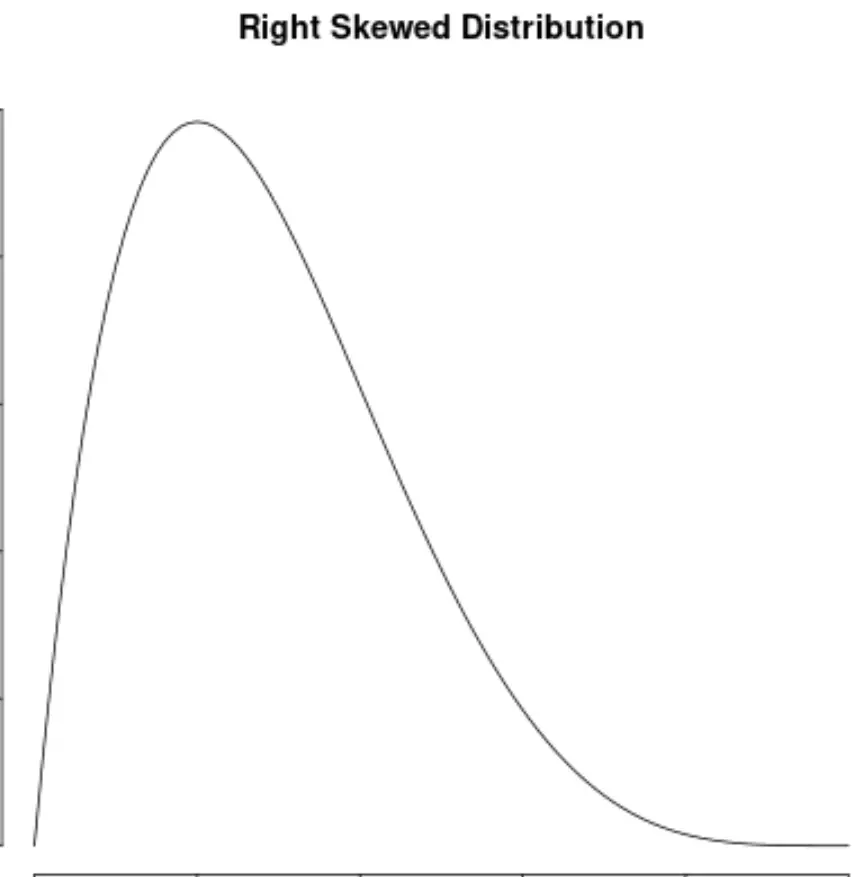
对称分布的性质

在对称分布中，均值、中位数和众数都相等。

请记住以下每个定义：

• 平均值：平均值。
• 中位数：平均值。
• 众数：最常出现的值。

在对称分布中，这些值彼此相等。

到目前为止，在每个示例中，我们都使用单峰分布作为示例——只有一个“峰值”的分布。然而，分布也可以是双峰和对称的。

双峰分布是具有两个峰值的分布。

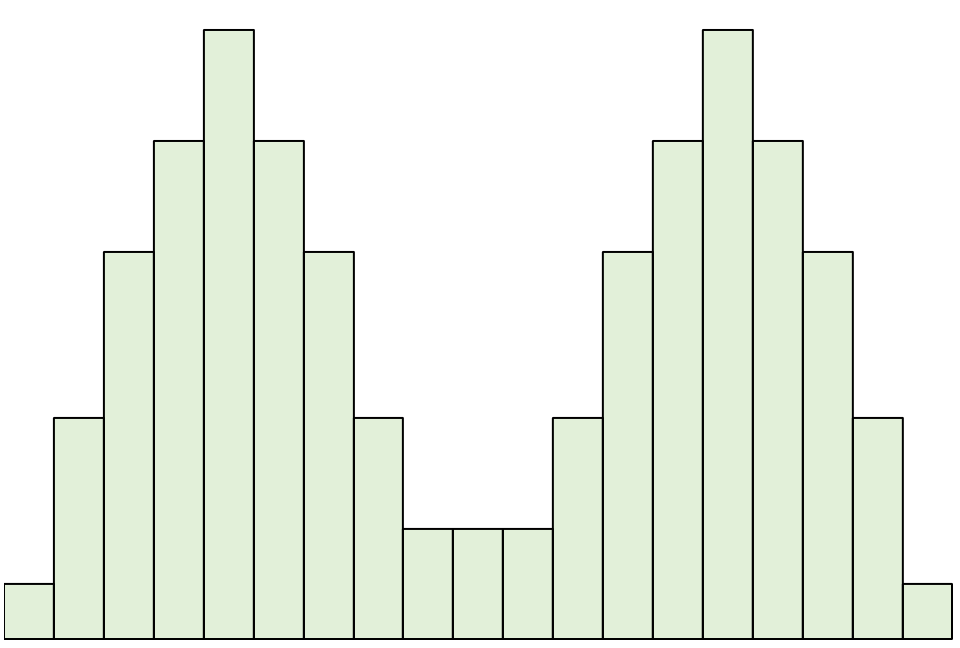
请注意，如果我们沿着该分布的中心画一条线，左侧和右侧仍然会相互镜像。

对于这些分布，平均值和中位数相等。然而，众数位于两个顶点。

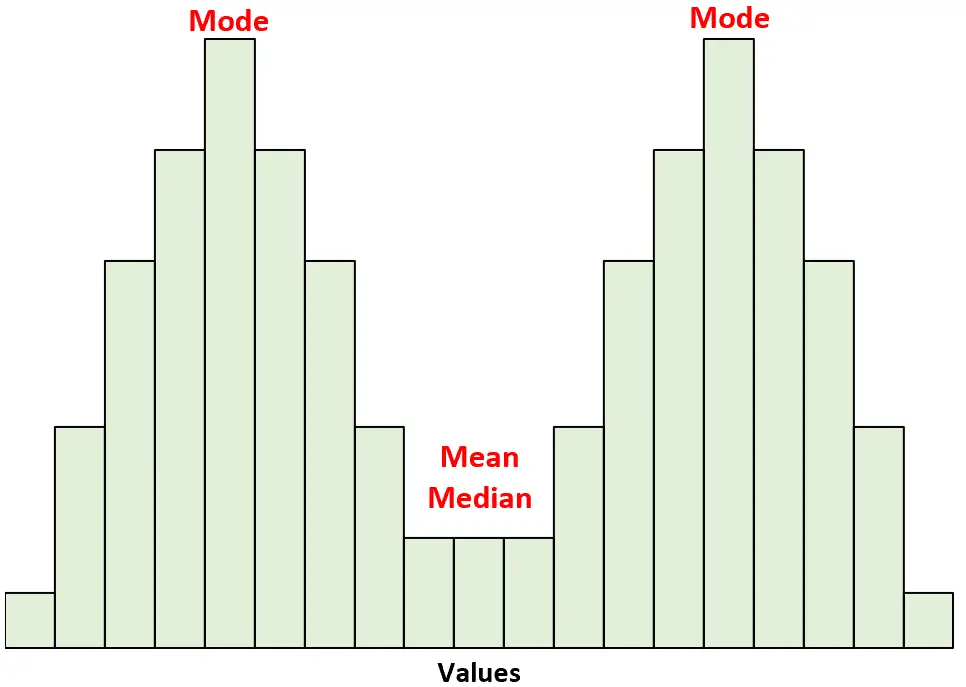
对称分布的其他示例

除了正态分布外，以下分布也是对称的：

分布t

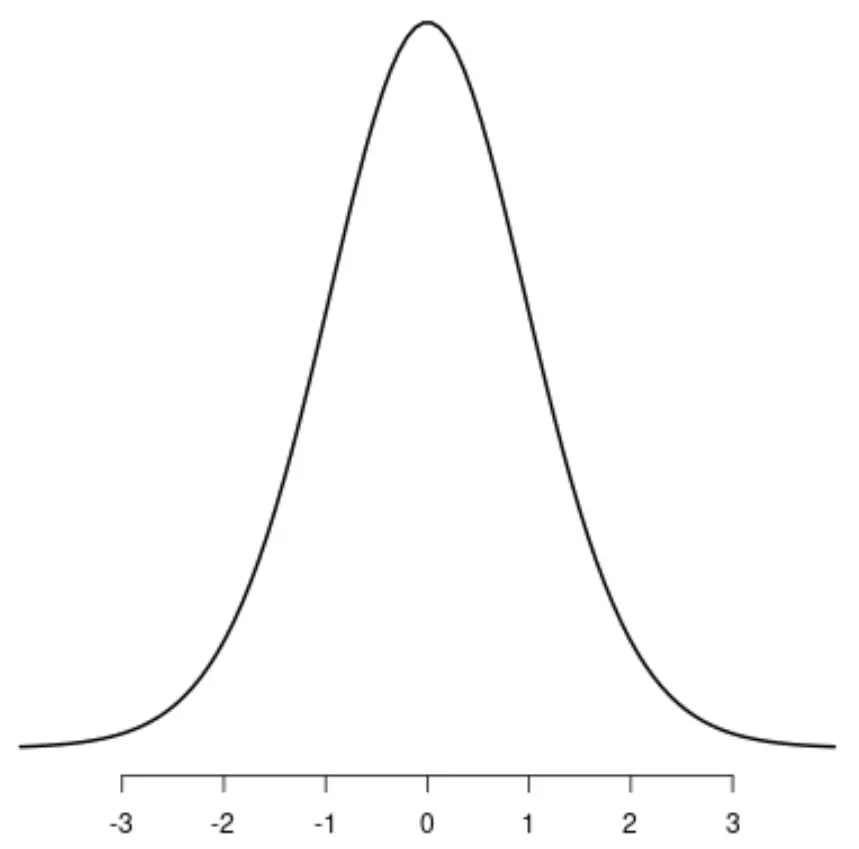
均匀分布

柯西分布

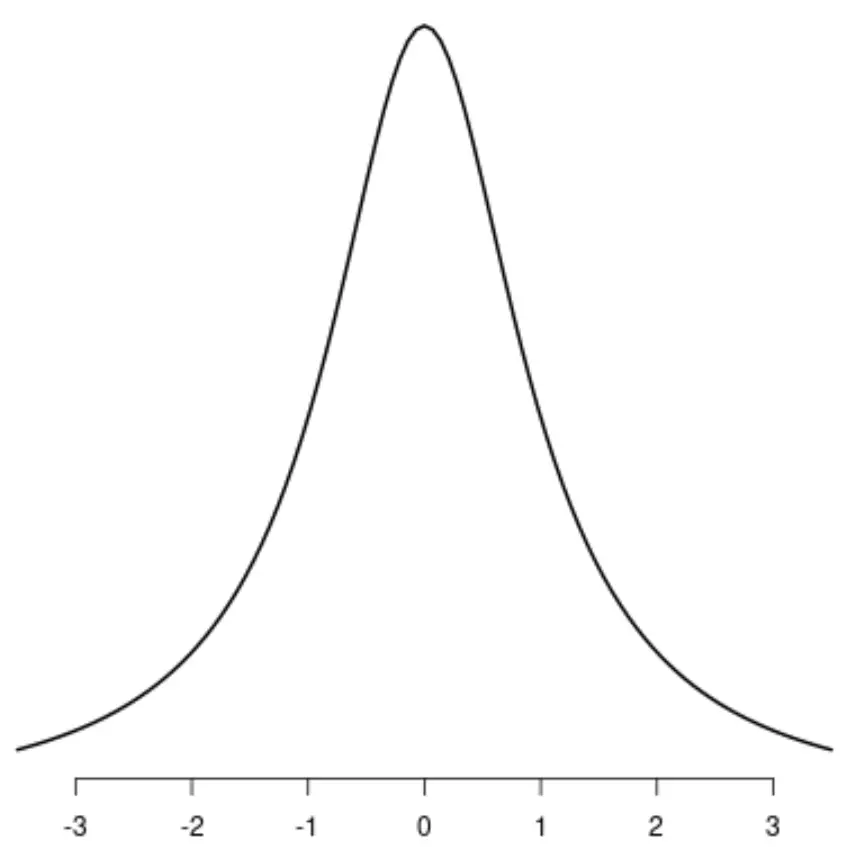
如果您在其中一个分布的中心画一条线，则每个分布的左侧和右侧将完美地相互镜像。

对称分布和中心极限定理

所有统计学中最重要的定理之一是中心极限定理，该定理指出，如果样本量足够大，即使总体分布不正态，样本均值的抽样分布也近似正态。

为了应用中心极限定理，样本量必须足够大。事实证明，到底有多少人“足够大”取决于人口分布的基本形状。

尤其：

• 如果总体分布是对称的，有时小至 15 个样本就足够了。
• 如果人口分布存在偏差，通常需要至少 30 人的样本。
• 如果人口分布极度不均，则可能需要 40 人或更多人的样本。

所以对称分布的优点是我们在计算置信区间或进行假设检验时需要较小的样本量来应用中心极限定理。

其他资源

中心极限定理简介
什么是双峰分布？
左右偏态分布指南