平均值与标准差之间的关系（举例）
平均值表示一组数据的平均值。
计算方法如下：
样本均值 = Σx i / n
金子：
- Σ：表示“和”的符号
- x i ：数据集中的第 i个观察值
- n：数据集中的观测总数
标准差表示数据集中值相对于平均值的分布。
计算方法如下：
样本标准差 = √ Σ( xi – x bar ) 2 / (n-1)
金子：
- Σ：表示“和”的符号
- x i :样本的第 i 个值
- x bar :样本平均值
- n：样本量
注意平均值和标准差之间的关系：公式中使用平均值来计算标准差。
事实上，除非我们知道样本均值，否则我们无法计算样本的标准差。
以下示例展示了如何在实践中计算数据集的样本均值和样本标准差。
示例：计算数据集的平均值和标准差
假设我们有以下数据集，显示 10 名不同篮球运动员的得分：
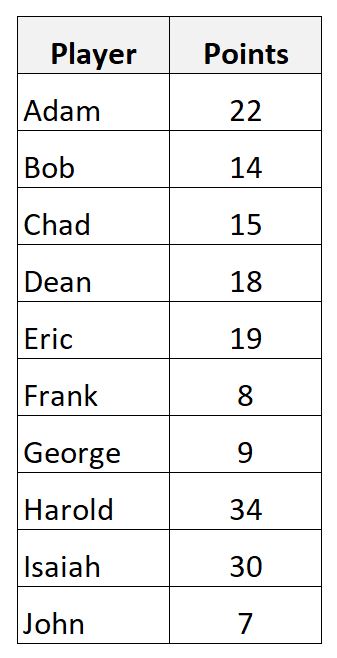我们可以使用以下公式计算样本平均得分：
- 样本均值 = Σx i / n
- 样本平均值 = (22+14+15+18+19+8+9+34+30+7) / 10
- 样本平均值 = 17.6
样本平均得分为17.6 分。这代表所有玩家的平均得分。
一旦我们知道了样本均值，我们就可以将其代入公式来计算样本标准差：
- 样本标准差 = √ Σ( xi – x bar ) 2 / (n-1)
- 样本标准差 = √ ((22-17.6) 2 + (14-17.6) 2 + (15-17.6) 2 + (18-17.6) 2 + (19-17.6) 6) 2 + (8-17.6) 2 + (9 -17.6) 2 + (34-17.6) 2 + (30-17.6) 2 + (7-17.6) 2 ) / (10-1)
- 样本标准差 = 9.08
样本标准差为9.08 。这表示每个点值与样本点平均值之间的平均距离。
了解数据集的平均值和标准差很有用，因为每个指标都告诉我们不同的信息。
平均值让我们了解数据集的“中心”值在哪里。
标准差让我们了解数据集中平均值周围的值分布。标准差值越高，样本中的值越分散。
通过了解这两个值，我们可以了解很多关于数据集中值的分布情况。
其他资源
以下教程提供有关平均值和标准差的其他信息：
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多