什么是抽样分布？

想象一下，有 10,000 只海豚，其中一只海豚的平均体重为 300 磅。

如果我们从这个种群中随机抽取 50 只海豚，我们可能会发现该样本中海豚的平均体重为 305 磅。

然后，如果我们再抽取 50 只海豚的简单随机样本，我们可能会发现该样本中海豚的平均体重为 295 磅。

每当我们对 50 只海豚进行简单随机抽样时，样本中海豚的平均体重很可能接近种群平均体重 300 磅，但又不完全是 300 磅。

假设我们从该种群中抽取 50 只海豚的 200 个简单随机样本，并创建每个样本平均体重的直方图：

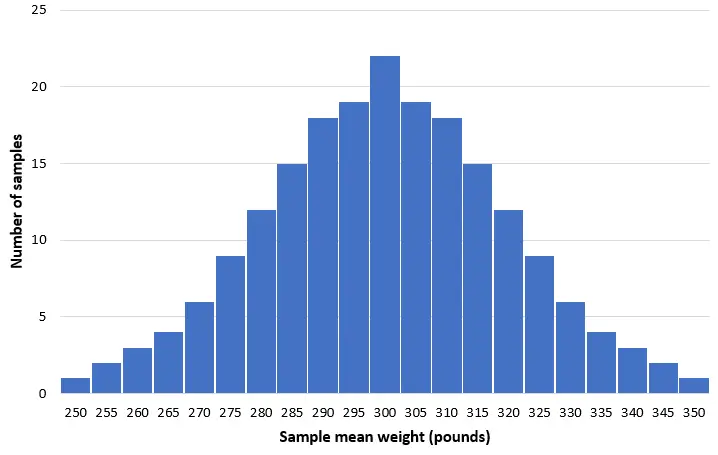
在大多数样本中，平均重量接近 300 磅。在极少数情况下，我们可能会采集大量平均体重仅为 250 磅的小海豚。或者我们可能会采集平均重 350 磅的宽吻海豚样本。一般来说，样本均值的分布近似正态，分布中心位于总体的真实中心。

样本均值的这种分布称为均值的抽样分布，并具有以下属性：

_µx = µ

其中 μ _x是样本平均值，μ 是总体平均值。

_σx = σ/√n

其中 σ _x是样本标准差，σ 是总体标准差，n 是样本量。

例如，在这个海豚种群中，我们知道平均体重为 μ = 300。因此采样分布的平均值为μ _x = 300 。

假设我们还知道总体标准差是 18 磅。因此，样本标准差为σ _x = 18/ √50 = 2.546 。

比例抽样分配

考虑同样数量的 10,000 只海豚。假设 10% 的海豚是黑色的，其余的是灰色的。假设我们对 50 只海豚进行了简单的随机抽样，发现该样本中 14% 的海豚是黑色的。接下来，我们再对 50 只海豚进行简单随机抽样，发现该样本中 8% 的海豚是黑色的。

想象一下，我们从该种群中抽取 50 只海豚的 200 个简单随机样本，并创建每个样本中黑海豚比例的直方图：

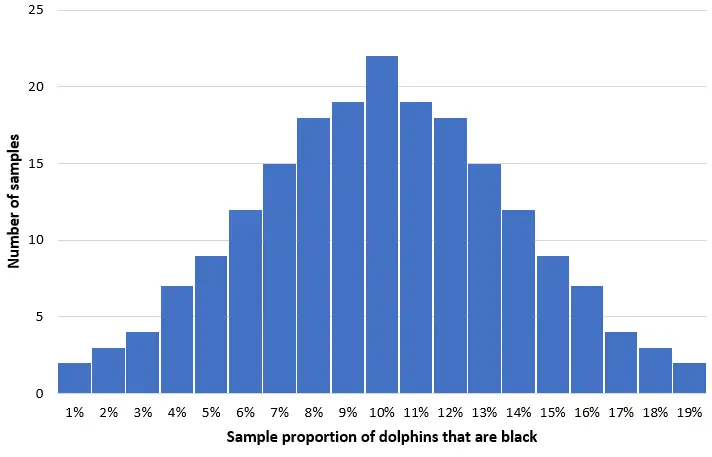
在大多数样本中，黑海豚的比例将接近实际种群的 10%。黑海豚的样本比例分布将近似正态分布，分布中心位于种群的真实中心。

这种样本比例分布称为比例抽样分布，具有以下属性：

_µp = P

其中p是样本比例， P是总体比例。

σ _p = √ (P)(1-P) / n

其中 P 是总体比例，n 是样本大小。

例如，在这个海豚种群中，我们知道黑海豚的真实比例是 10% = 0.1。因此，比例抽样分布的平均值为μ _p = 0.1 。

假设我们还知道总体标准差是 18 磅。因此，样本标准差为σ _p = √ (P)(1-P) / n = √ (.1)(1-.1) / 50 = .042 。

建立常态

要使用上面的公式，抽样分布必须是正态的。

根据中心极限定理，如果样本量足够大，即使总体分布不正态，样本均值的抽样分布也近似正态。在大多数情况下，我们认为 30 个或更多的样本量就足够大了。

如果预期成功次数和失败次数都至少为 10，则样本比例的抽样分布近似正态。

例子

我们可以使用抽样分布来计算概率。

示例1：某台机器创建cookie。这些饼干的重量分布向右倾斜，平均值为 10 盎司，标准差为 2 盎司。如果我们对这台机器生产的 100 块饼干进行简单随机抽样，则该样本中饼干的平均重量小于 9.8 盎司的概率是多少？

第一步：建立常态。

我们需要保证样本均值的抽样分布是正态的。由于我们的样本量大于等于30，根据中心极限定理，我们可以假设样本均值的抽样分布是正态的。

步骤 2：求抽样分布的均值和标准差。

_µx = µ

_σx = σ/√n

μ _x = 10 盎司

σ _x = 2/ √100 = 2/10 = 0.2 盎司

步骤 3：使用Z 分数面积计算器确定该样本中饼干的平均重量小于 9.8 盎司的概率。

将以下数字输入Z 分数面积计算器。您可以将“原始分数 2”留空，因为我们在此示例中只找到一个数字。

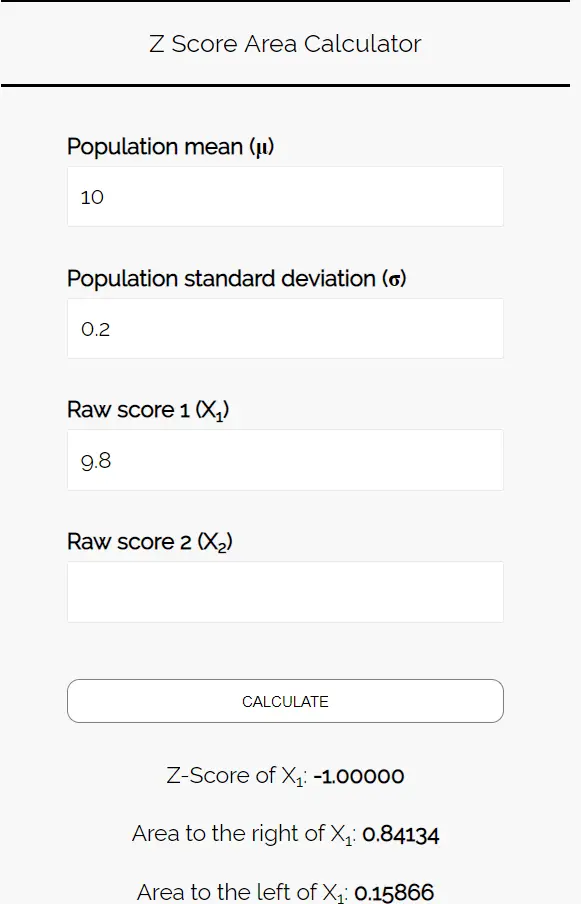
由于我们想知道此样本中饼干的平均重量小于9.8 盎司的概率，因此我们对 9.8左侧的区域感兴趣。计算器告诉我们这个概率是0.15866 。

示例 2：根据一项全校范围的研究，某所学校 87% 的学生更喜欢披萨而不是冰淇淋。假设我们对 200 名学生进行简单随机抽样。喜欢披萨的学生比例低于 85% 的概率是多少？

第一步：建立常态。

回想一下，如果“成功”和“失败”的预期数量都至少为 10，则样本比例的抽样分布近似正态。

在本例中，预计喜欢披萨的学生人数为 87% * 200 名学生 = 174 名学生。预计不喜欢披萨的学生人数为 13% * 200 名学生 = 26 名学生。由于这两个数字都至少为 10，我们可以假设喜欢披萨的学生比例的抽样分布近似正态分布。

步骤 2：求抽样分布的均值和标准差。

_µp = P

σ _p = √ (P)(1-P) / n

_微p = 0.87

σ _p = √ (0.87)(1-0.87) / 200 = 0.024

步骤 3：使用Z 分数面积计算器确定喜欢披萨的学生比例低于 85% 的概率。

将以下数字输入Z 分数面积计算器。您可以将“原始分数 2”留空，因为我们在此示例中只找到一个数字。

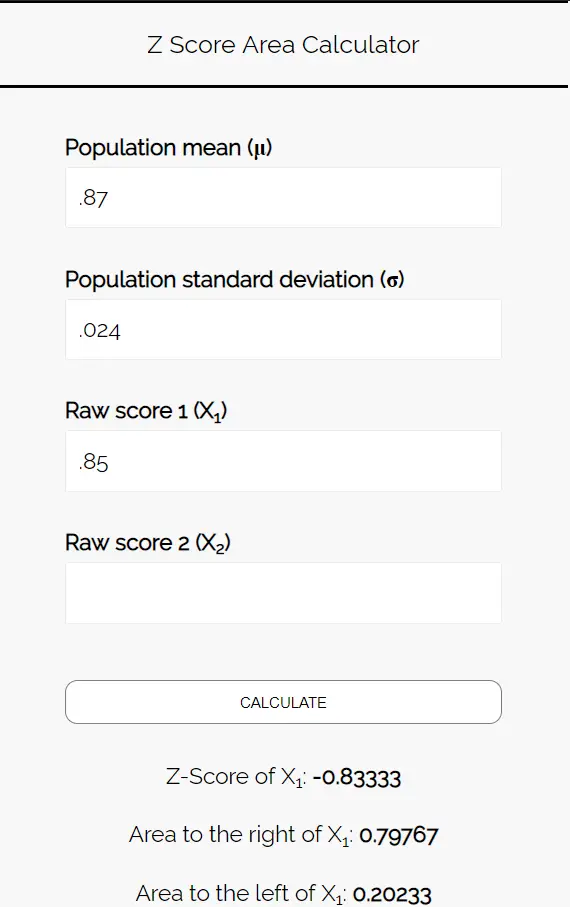
由于我们想知道喜欢披萨的学生比例低于 85% 的概率，因此我们对 0.85左侧的区域感兴趣。计算器告诉我们这个概率是0.20233 。