拟方差
本文解释了统计学中的拟方差是什么。因此,您将了解如何计算拟方差、已解决的练习以及拟方差和方差之间的差异。此外,您可以使用在线计算器计算任何数据集的拟方差。
什么是拟方差?
在统计学中,准方差是指示样本变异性的离散度度量。更准确地说,准方差等于偏差的平方和除以观测值总数减一。
拟方差的符号是
![]()
任何一个
![]()
。有时虽然也使用该符号
![]()
来表示拟方差。
拟方差用于确定样本的离散度,同时避免偏差,这就是为什么它通常被称为无偏方差。因此,拟方差是总体方差的良好估计量。事实上,在计算样本方差时,常常使用拟方差公式来代替方差公式。下面我们将详细介绍这两种统计指标之间的差异。
拟方差公式
要计算拟方差,需要找到数据集的值与平均值之间的差的平方和,然后将其除以数据总数减一。
因此,计算拟方差的公式如下:

金子:
-
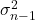
是拟方差。
-

是数据值

。
-

是数据总数。
-

是数据集的平均值。
👉您可以使用下面的计算器来计算任何数据集的拟方差。
您可能想知道为什么它除以 n-1 而不是除以 n?嗯,这是为了消除偏差,这样我们就得到了一个无偏估计量。这正是为什么准方差是总体方差的良好估计量的原因。
拟方差计算示例
现在我们知道了拟方差的定义,我们将解决一个简单的示例,以便您了解如何计算数据序列的拟方差。
- 从一家跨国公司,我们知道它在过去五年中所取得的经济成果,大部分都获得了利润,但有一年却出现了相当大的损失:11.5, 2, -9, 700 万欧元。计算该数据集的拟方差。
要获得数据集的拟方差,我们需要做的第一件事是计算其算术平均值:
![]()
一旦我们知道了数据的平均值,我们就应用拟方差公式:
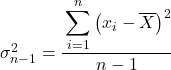
因此,我们将练习指导提供的数据代入公式:
![]()
最后,解决计算拟方差的运算就足够了:
![Rendered by QuickLaTeX.com \begin{aligned}\sigma_{n-1}^2&=\cfrac{7,8^2+1,8^2+(-1,2)^2+(-12,2)^2+3,8^2}{5}\\[2ex]&=\cfrac{60,84+3,24+1,44+148,84+14,44}{5-1}\\[2ex]&= \cfrac{228,8}{4} \\[2ex]&=57,2 \ \text{millones de euros}^2\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5d64d58e69b766d9075ec1220386d8c0_l3.png)
请注意,拟方差的单位与统计数据的单位相同,但为平方,因此该数据集的拟方差为 5720 万2 。
拟方差计算器
将统计数据集输入以下计算器以计算其准方差。数据必须用空格分隔,并使用句点作为小数点分隔符输入。
方差和拟方差
最后,我们将看到准方差和方差之间的区别,因为尽管它们的名称相似,但它们的计算方式也非常相似。
准方差和方差之间的差是公式的分母。要计算拟方差,必须除以 n-1,但是方差是通过除以 n 计算的。
因此,准方差和方差在数学上是相关的,因为准方差等于方差乘以 n(数据点总数)并除以 n-1。
![]()
因此,对于同一数据集,拟方差值将始终大于方差值。