斯特奇斯是什么？统治者？ （定义&#038；示例）

直方图是一种帮助我们可视化一组数据中值的分布的图表。

事实证明，直方图中使用的方框数量会对我们解释数据的方式产生巨大影响。

如果我们使用的组太少，数据中真正的底层模式可能会被隐藏：

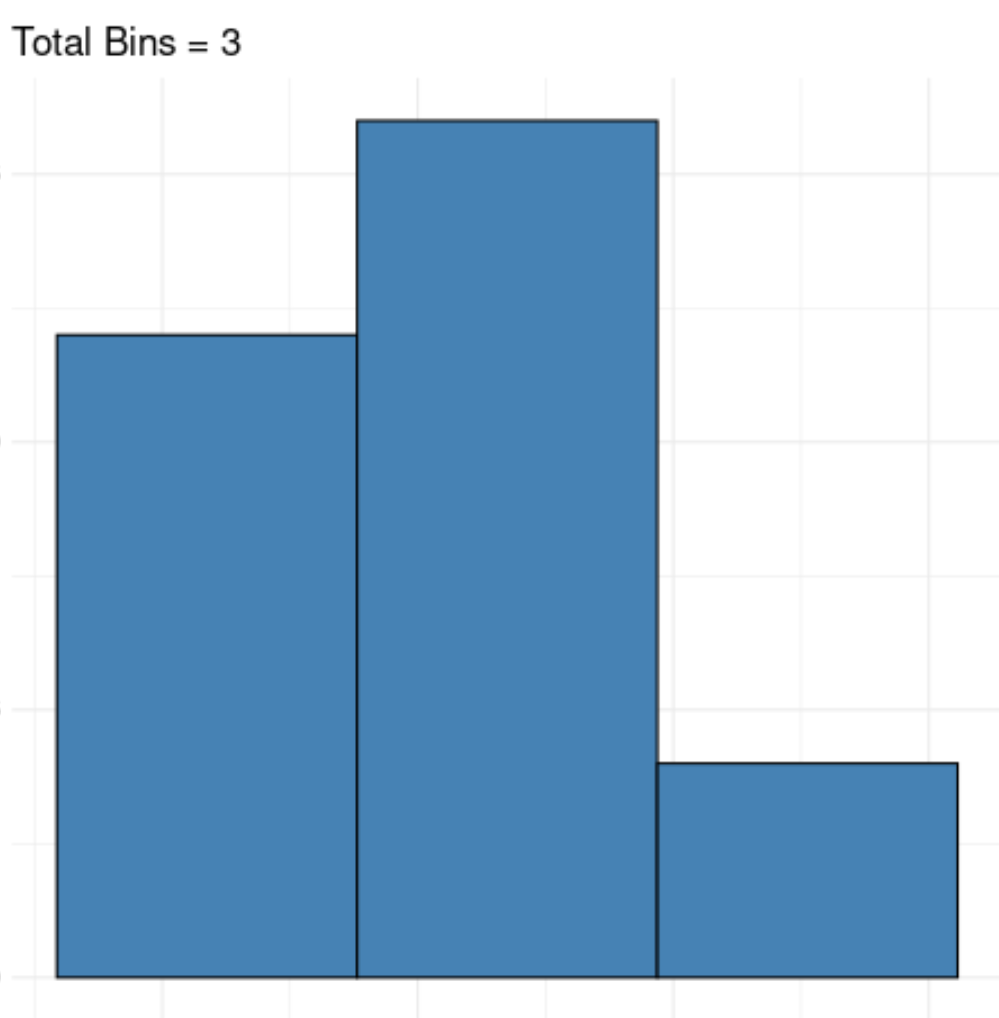
如果我们使用太多组，我们可以简单地可视化数据集中的噪声：

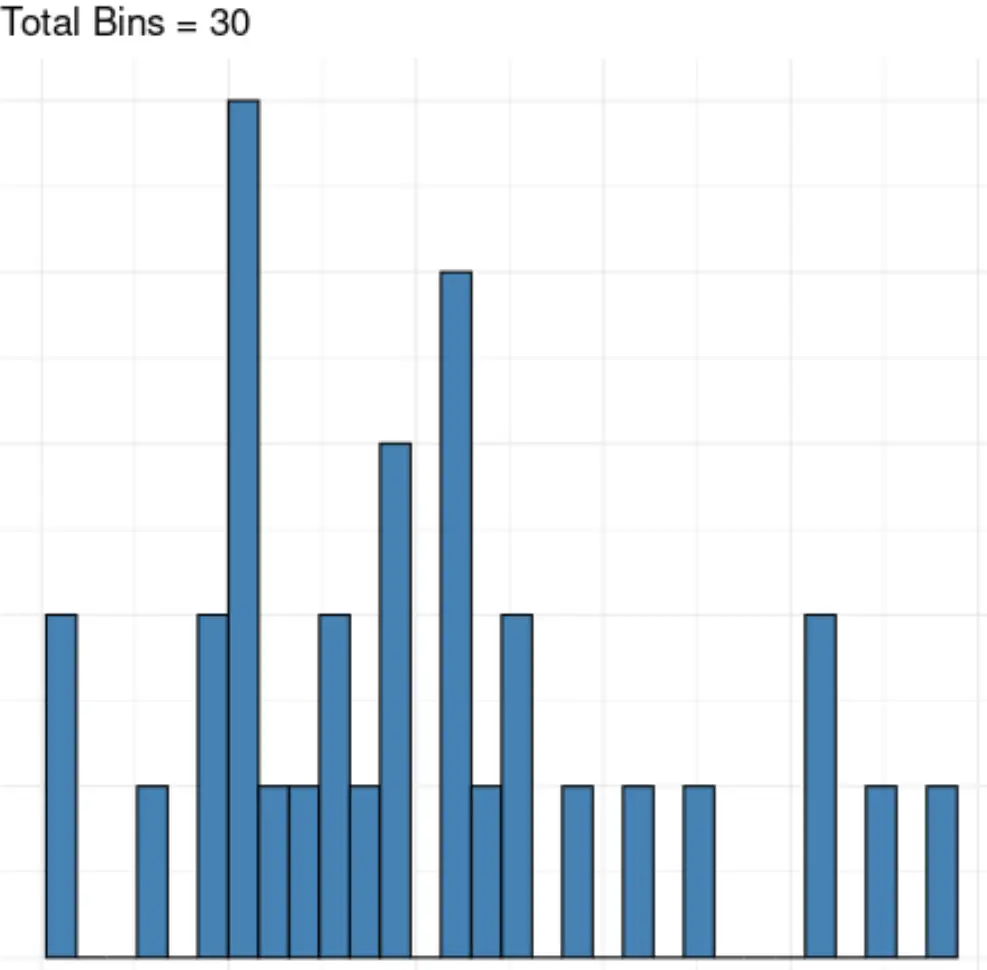
幸运的是，我们可以使用一种称为斯特吉斯规则的方法来确定直方图中使用的最佳框数。

斯特吉斯规则使用以下公式来确定直方图中使用的最佳组数：

最佳 bin = ⌈log ₂ n + 1⌉

金子：

• n：数据集中的观测总数。
• ⌈ ⌉：表示“上限”的符号，即将答案四舍五入到最接近的整数。

示例：斯特吉斯规则

假设我们有以下数据集，总共有 n = 31 个观测值：

我们可以使用斯特吉斯规则来确定用于在直方图中可视化这些值的最佳框数：

最佳 bin = ⌈log ₂ (31) + 1⌉ = ⌈4.954 + 1⌉ = ⌈5.954⌉ = 6 。

根据 Sturges 规则，我们应该在直方图中使用 6 个箱来可视化该值的分布。

对于该数据集，包含 6 个组的直方图如下所示：

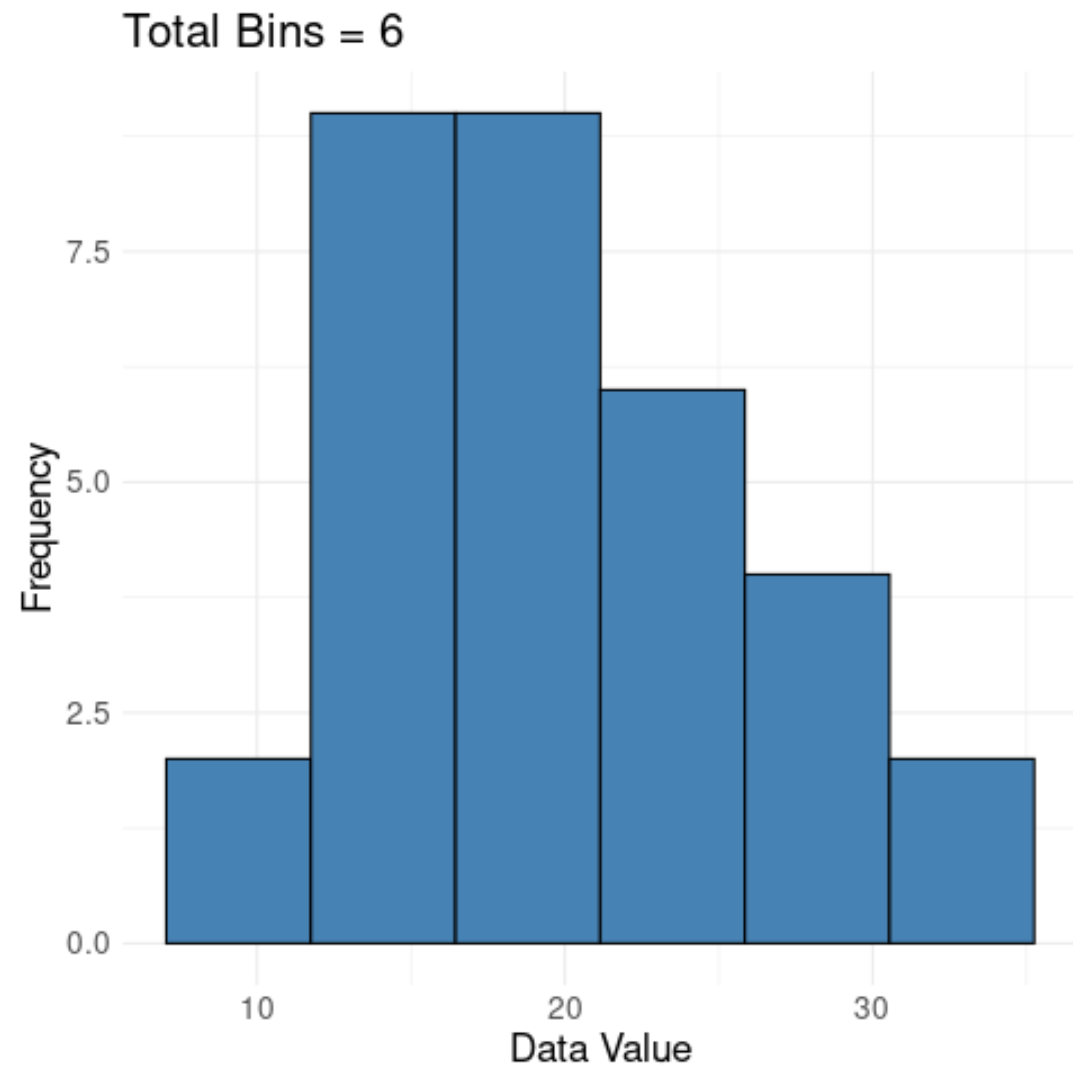
请注意，这似乎足以很好地了解值的基本分布，而不会因为数量太多而无法简单地可视化数据中的噪声。

斯特奇斯规则的共同价值观

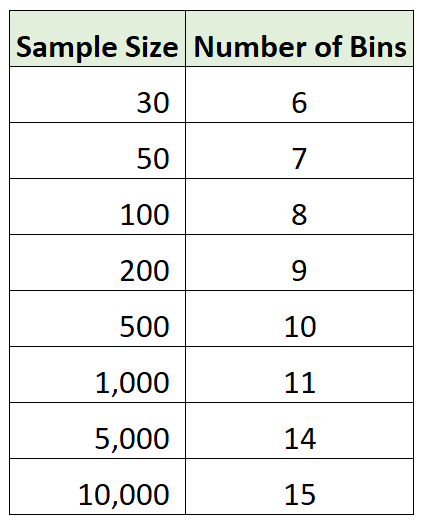
下表显示了根据斯特吉斯规则，基于数据集中的观测总数的直方图中使用的最佳组数：

斯特奇斯规则的替代方案

斯特吉斯规则是确定直方图中使用的最佳箱数的最常用方法，但还有多种替代方法，包括：

平方根规则：盒子数量 = ⌈√ n ⌉

大米规则：箱数 = ⌈2 * ³ √ n ⌉

Freedman-Diaconis 规则：框数 = (2*IQR) / ³ √ n其中IQR是四分位数范围。

奖励：斯特吉斯规则计算器

使用此免费在线计算器自动应用斯特吉斯规则，根据数据集的大小确定用于直方图的最佳组数。