方差分析与回归：有什么区别？
统计学中两种常用的模型是方差分析和回归模型。
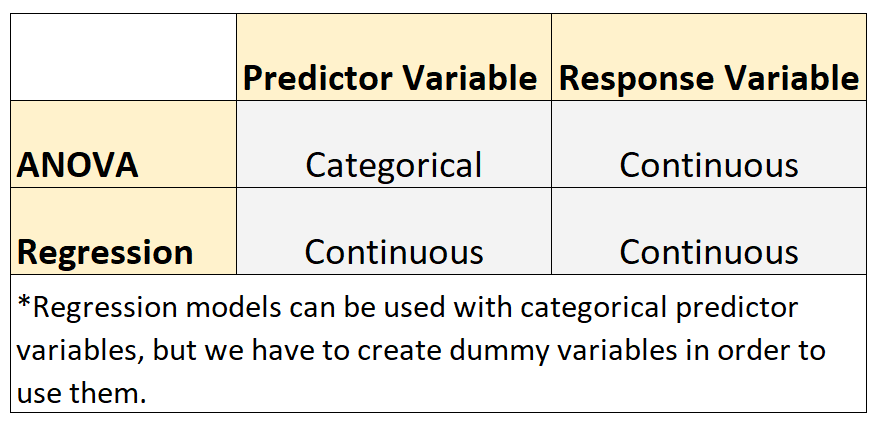
这两类模型有以下相似之处：
- 每个模型中的响应变量都是连续的。连续变量的例子包括体重、高度、长度、宽度、时间、年龄等。
然而，这两种类型的模型有以下区别：
- 当预测变量是分类变量时，使用方差分析模型。分类变量的例子包括教育水平、眼睛颜色、婚姻状况等。
- 当预测变量连续时使用回归模型。*
*回归模型可以与分类预测变量一起使用，但我们需要创建虚拟变量才能使用它们。
以下示例说明了何时在实践中使用方差分析或回归模型。
示例 1：首选方差分析模型
假设一位生物学家想要了解四种不同的肥料是否会在一个月内导致相同的平均植物生长（以英寸为单位）。为了测试这一点，她将每种肥料施用于 20 株植物，并在一个月后记录每株植物的生长情况。
在这种情况下，生物学家必须使用单向方差分析模型来分析肥料之间的差异，因为存在预测变量并且是分类变量。
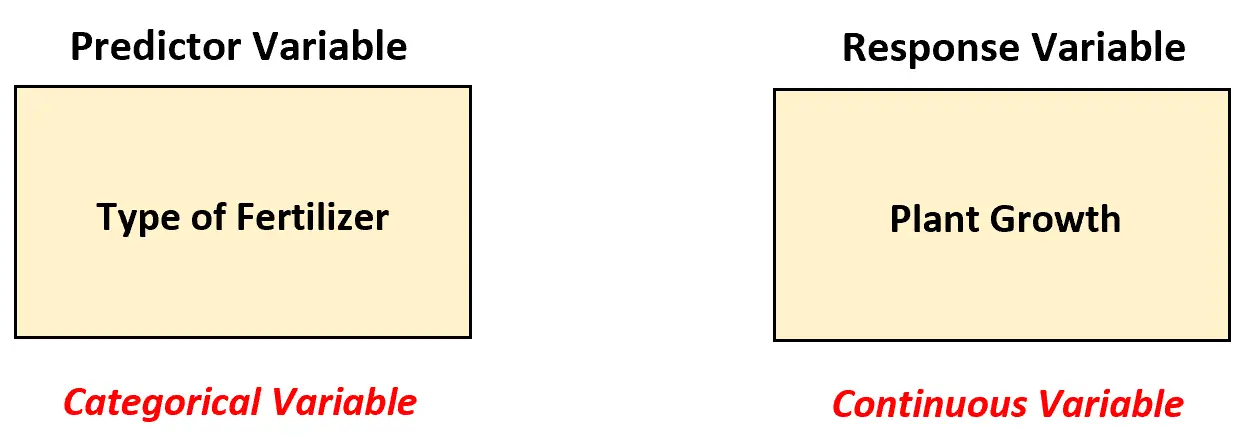
换句话说，预测变量的值可以分为以下“类别”：
- 肥料1
- 肥料2
- 肥料3
- 肥料4
单向方差分析将告诉生物学家四种不同肥料之间的平均植物生长是否相等。
示例 2：首选回归模型
假设一位房地产经纪人想要了解平方英尺和房地产价格之间的关系。为了分析这种关系，他收集了特定城市 200 套房屋的面积和价格数据。
在这种情况下，房地产经纪人应使用简单的线性回归模型来分析这两个变量之间的关系，因为预测变量（平方英尺）是连续的。
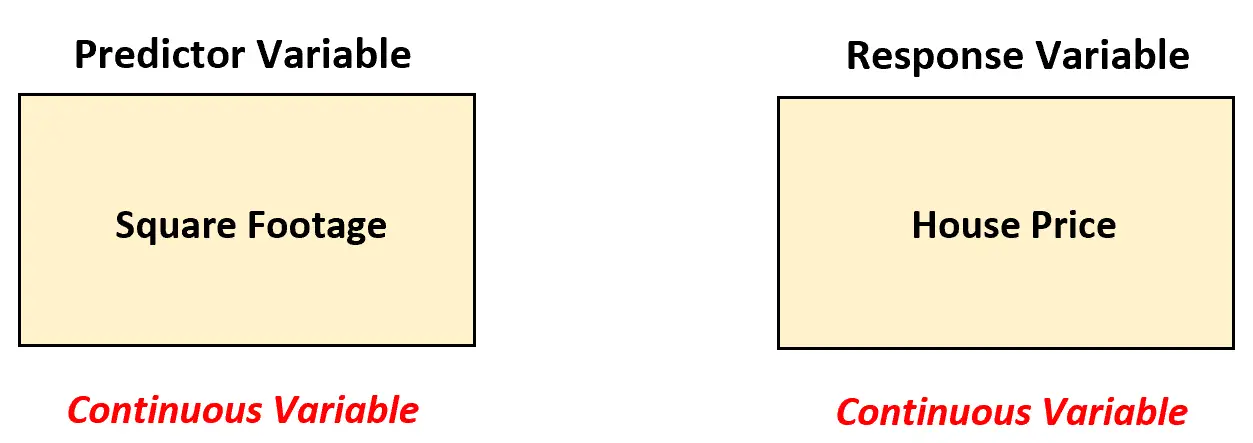
使用简单线性回归，房地产经纪人可以拟合以下回归模型：
房地产价格 = β 0 + β 1 (平方面积)
β 1的值将代表与每增加平方英尺相关的房价的平均变化。
这将使房地产经纪人能够量化平方英尺和房价之间的关系。
示例 3：具有首选虚拟变量的回归模型
假设房地产经纪人想要了解预测变量“平方英尺”和“房屋类型”（单户、公寓、联排别墅）与房地产价格响应变量之间的关系。
在这种情况下，房地产经纪人可以通过将“房屋类型”转换为虚拟变量来使用多元线性回归，因为它当前是分类变量。
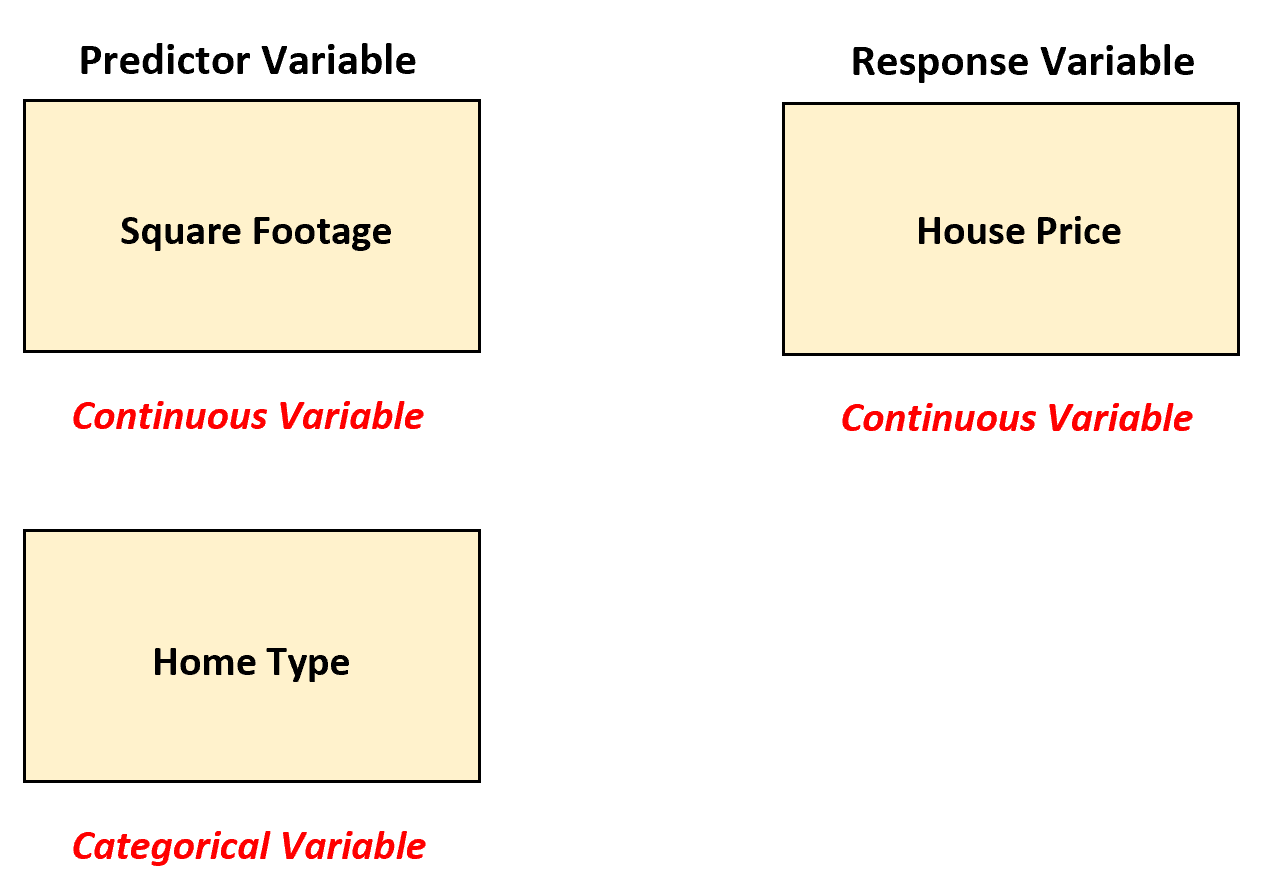
然后，房地产经纪人可以拟合以下多元线性回归模型：
房地产价格 = β 0 + β 1 (平方面积) + β 2 (独栋) + β 3 (公寓)
以下是我们解释模型系数的方式：
- β 1 ：与增加一平方英尺相关的房价平均变化。
- β 2 ：假设面积保持不变，单户住宅和联排别墅之间的平均价格差异。
- β 3 ：假设表面积不变，单户住宅和公寓之间的平均价格差异。
查看以下教程，了解如何在不同的统计软件中创建虚拟变量：
其他资源
以下教程深入介绍了 ANOVA 模型：
以下教程深入介绍了线性回归模型：
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多