重复测量方差分析：定义、公式和示例

重复测量方差分析用于确定三个或更多组的平均值之间是否存在统计显着性差异，其中每组中出现相同的受试者。

重复测量方差分析通常用于两种特定情况：

1. 测量受试者在三个或更多时间点的平均分数。例如，您可能想要在开始训练计划前一个月、训练计划中间以及训练计划后一个月测量受试者的静息心率，看看平均静息心率是否有显着差异。这三个时间点的比率。

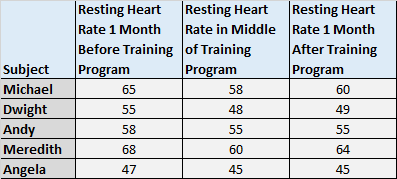
请注意相同的主题如何一遍又一遍地出现。我们重复测量相同的受试者，因此我们使用重复测量方差分析。

2. 测量受试者在三种不同条件下的平均分数。例如，您可能会要求受试者观看三部不同的电影，并根据他们对电影的喜爱程度对每部电影进行评分。

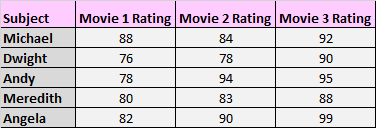
同样，每组中出现相同的受试者，因此我们需要使用重复测量方差分析来测试这三种条件之间的均值差异。

单向方差分析与重复测量方差分析

在典型的 单向方差分析中，每组使用不同的主题。例如，我们可以要求受试者对三部电影进行评分，如上例所示，但我们使用不同的受试者对每部电影进行评分：

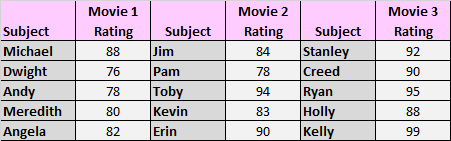
在这种情况下，我们将执行典型的单向方差分析来测试三部电影的平均评分之间的差异。

在现实生活中，在多种治疗条件下使用相同的受试者有两个优点：

1.对于研究人员来说，招募和支付较少数量的人来进行实验会更便宜、更快捷，因为他们可以多次从同一个人那里获取数据。

2.我们能够将数据中的一些方差归因于受试者本身，从而更容易获得较小的 p 值。

这种设计的一个潜在缺点是，如果实验持续太长时间，受试者可能会感到无聊或疲劳，这可能会扭曲结果。例如，受试者可能会对他们观看的第三部电影评分较低，因为他们累了并准备回家。

重复测量方差分析：示例

假设我们招募五名受试者参加培训计划。我们在参加训练计划前、参加训练计划 4 个月后和参加训练计划 8 个月后测量他们的静息心率。

下表显示了结果：

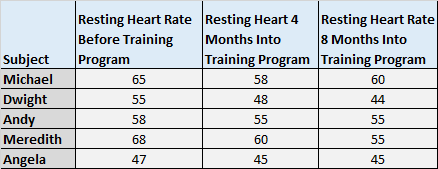
我们想知道这三个时间点的平均剩余心率是否存在差异。因此，我们使用以下步骤在 0.05 显着性水平上执行重复测量方差分析：

步骤 1. 陈述假设。

原假设 (H ₀ )： µ ₁ = µ ₂ = µ ₃ （总体平均值均相等）

备择假设：(Ha)：至少一个总体均值与其他总体均值不同

步骤 2. 执行重复测量方差分析。

我们将使用重复测量方差分析计算器并使用以下输入：

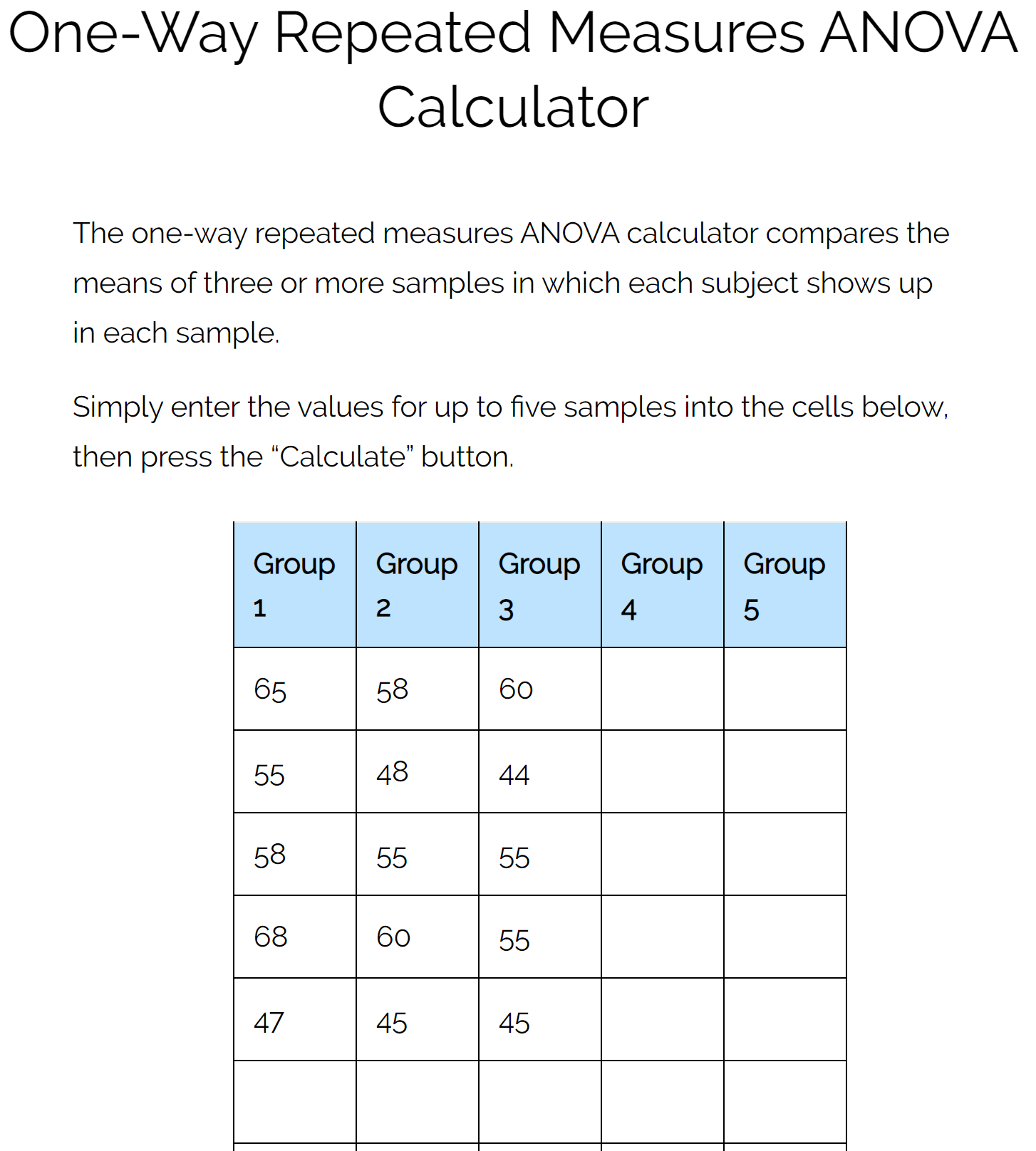
一旦我们点击“计算”，就会自动出现以下结果：

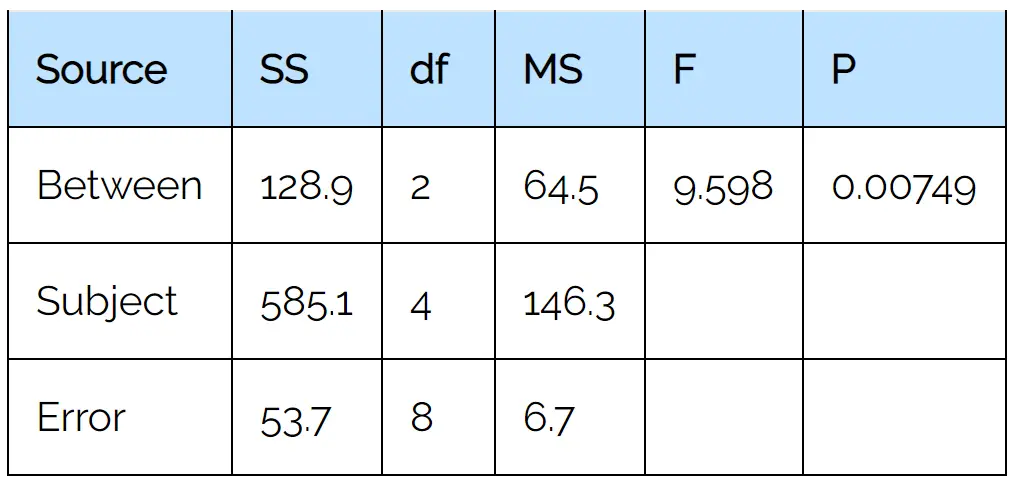
步骤 3.解释结果。

从输出表中，我们看到 F 检验统计量为9.598 ，相应的 p 值为0.00749 。

由于该 p 值小于 0.05，因此我们拒绝原假设。这意味着我们有足够的证据表明三个不同时间的平均剩余心率之间存在统计上的显着差异。

其他资源

以下文章解释了如何使用不同的统计软件执行重复测量方差分析：

Excel 中的重复测量方差分析
R 中的重复测量方差分析
Stata 中的重复测量方差分析
Python 中的重复测量方差分析
SPSS 中的重复测量方差分析
Google 表格中的重复测量方差分析
手重复测量方差分析
重复测量方差分析计算器