如何在 stata 中执行多元方差分析
单向方差分析用于确定解释变量的不同水平是否会导致某些响应变量出现统计上不同的结果。
例如,我们可能有兴趣了解三个教育级别(副学士学位、学士学位、硕士学位)是否会导致年收入在统计上有所不同。在这种情况下,我们有一个解释变量和一个响应变量。
- 解释变量:教育水平
- 响应变量:年收入
多元方差分析是单向方差分析的扩展,其中有多个响应变量。例如,我们可能有兴趣了解教育水平是否会导致不同的年收入和不同数量的学生债务。在这种情况下,我们有一个解释变量和两个响应变量:
- 解释变量:教育水平
- 响应变量:年收入、学生债务
由于我们有多个响应变量,因此在这种情况下使用多元方差分析是合适的。
接下来,我们将解释如何在 Stata 中执行多元方差分析。
示例:Stata 中的多元方差分析
为了说明如何在 Stata 中执行多元方差分析,我们将使用以下数据集,其中包含 24 人的以下三个变量:
- educ:学习水平(0 = 副学士学位,1 = 学士,2 = 硕士)
- 收入:年收入
- 债务:学生贷款债务总额
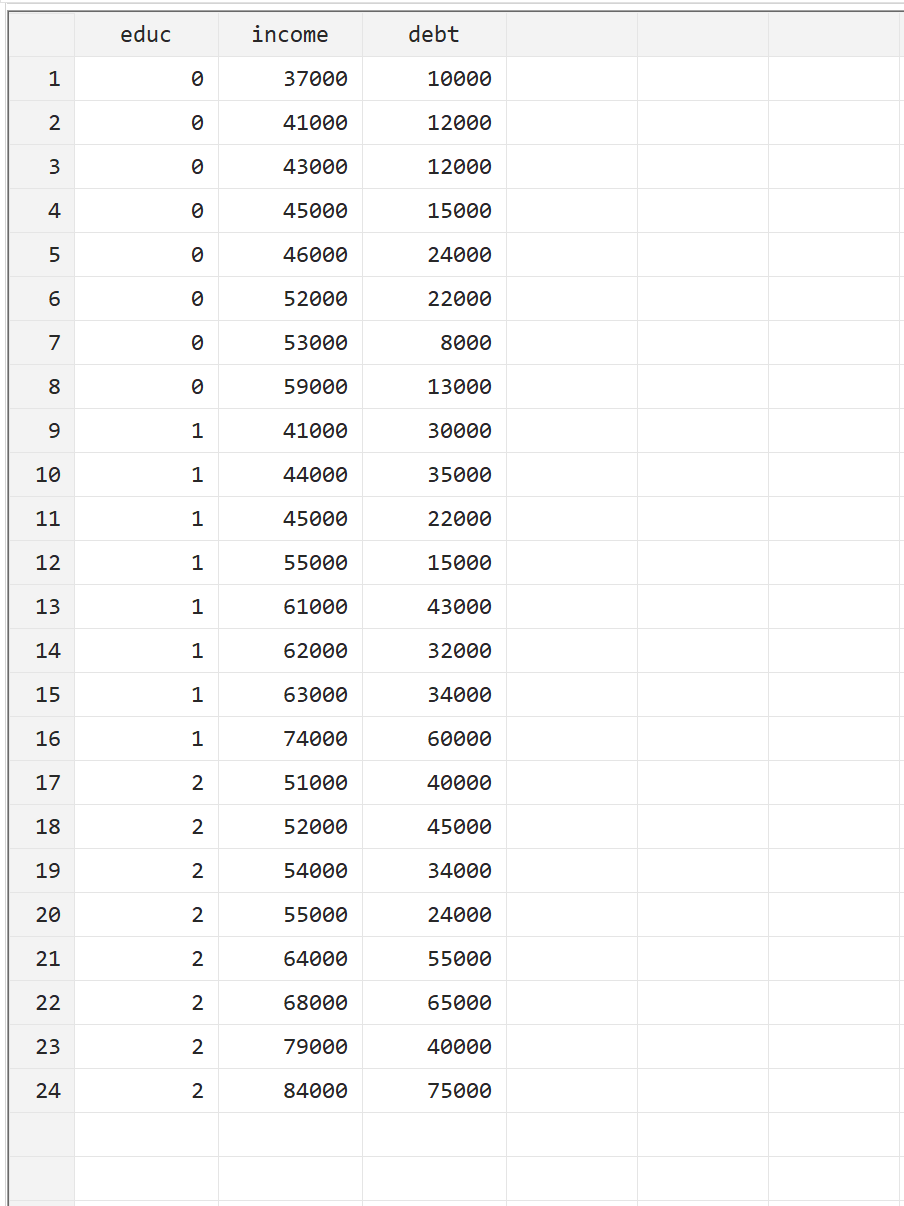
您可以通过导航到顶部菜单栏中的数据 > 数据编辑器 > 数据编辑器(编辑)来手动输入数据来重现此示例。
要使用教育作为解释变量、收入和债务作为响应变量来执行多元方差分析,我们可以使用以下命令:
收入债务多元方差 = educ

Stata 生成四个独特的检验统计量及其相应的 p 值:
Wilks 的 lambda: F 统计量 = 5.02,P 值 = 0.0023。
Pillai 迹线: F 统计量 = 4.07,P 值 = 0.0071。
Lawley-Hotelling 迹线: F 统计量 = 5.94,P 值 = 0.0008。
最大 Roy 根: F 统计量 = 13.10,P 值 = 0.0002。
有关如何计算每个检验统计量的详细说明,请参阅宾夕法尼亚州立大学埃伯利科学学院的这篇文章。
每个检验统计量的 p 值都小于 0.05,因此无论您使用哪一个,原假设都将被拒绝。这意味着我们有足够的证据表明,教育水平导致年收入和学生债务总额存在统计上的显着差异。
p 值注释:输出表中 p 值旁边的字母表示 F 统计量的计算方式(e = 精确计算,a = 近似计算,u = 上限)。