如何计算x^2的期望值

对于随机变量，表示为 X ，可以使用以下公式计算 X ²的期望值：

E(X ² ) = Σx ² * p(x)

金子：

• Σ ：表示“和”的符号
• x ：随机变量的值
• p(x) ：随机变量取给定值的概率

下面的例子展示了如何在实践中使用这个公式。

示例：计算 X ²的期望值

假设我们有以下概率分布表，描述随机变量的概率，

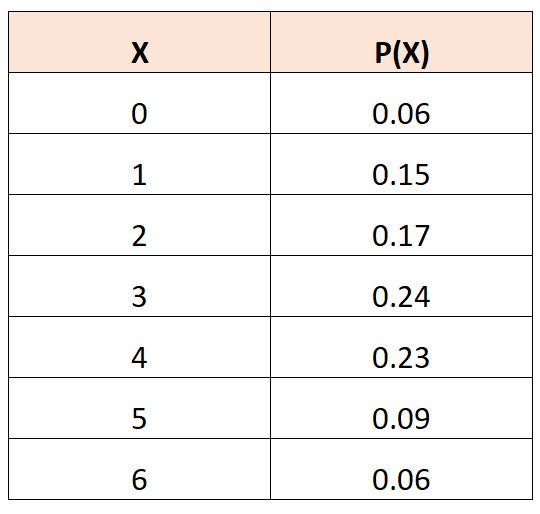
为了计算 X ²的期望值，我们可以使用以下公式：

E(X ² ) = Σx ² * p(x)

E(X ² ) = (0) ² *.06 + (1) ² *.15 + (2) ² *.17 + (3) ² *.24 + (4) ² *.23 + (5) ² *.09 + (6) ² *.06

E(X ² ) = 0 + 0.15 + 0.68 + 2.16 + 3.68 + 2.25+ 2.16

E( ^X2 ) = 11.08

X ²的期望值为11.08 。

请注意，此随机变量是离散随机变量，这意味着它只能采用有限数量的值。

如果X是连续随机变量，我们必须使用以下公式计算X ²的期望值：

E(X ² ) = ∫ x ² f(x)dx

金子：

• ∫：表示“整合”的符号
• f(x) : pdf继续用于随机变量

当计算连续随机变量的^X2期望值时，我们通常使用统计软件，因为手动执行此计算可能更困难。

其他资源

以下教程解释了如何执行统计中的其他常见任务：

如何找到概率分布的平均值
如何找到概率分布的标准差
如何求概率分布的方差