本杰明-霍赫伯格手术指南

任何时候执行统计检验时，即使您的原假设为真，您也有可能纯属偶然地获得小于 0.05 的 p 值。

例如，假设您想知道某种植物的平均高度是否大于 10 英寸。您用于测试的原假设和替代假设是：

H ₀ : μ = 10 英寸

H _A : μ > 10 英寸

为了检验这个假设，您可以出去随机收集 20 种植物样本进行测量。即使该植物物种的真实平均高度为 10 英寸，您也可能选择了 20 株异常高的植物作为样本，导致您拒绝原假设。

即使原假设为真（该植物的平均高度实际上为 10 英寸），您也拒绝了它。在统计学中，我们称之为“错误发现”。你声称已经有了一个发现——一个“重大成果”——但这实际上是错误的。

现在想象一下同时运行 100 个统计测试。使用 0.05 的alpha 水平时，单个测试出现错误发现的可能性只有 5%，但由于您正在进行大量测试，因此您预计 100 次测试中只有大约 5 次会导致错误发现。

在现代世界，错误发现可能是一个常见问题，因为技术允许研究人员一次执行数百甚至数千个统计测试。

例如，医学研究人员可以一次对数万个基因进行统计测试。即使错误发现率仅为 5%，这也意味着数百次测试可能会导致错误发现。

控制错误发现率的一种方法是使用所谓的Benjamini-Hochberg 程序。

本杰明-霍赫伯格程序

本杰明尼-霍赫伯格程序的工作原理如下：

第 1 步：执行所有统计测试并找到每个测试的 p 值。

步骤 2：按降序对 p 值进行排名，为每个值指定一个排名：最小值的排名为 1，次小的值的排名为 2，依此类推。

步骤 3：使用公式(i/m)*Q计算每个 p 值的临界 Benjamini-Hochberg 值

金子：

i = p 值的排名

m = 测试总数

Q = 您选择的错误发现率

步骤 4：找到小于临界值的最大 p 值。将小于此 p 值的每个 p 值指定为显着。

以下示例说明了如何使用具体值执行此过程。

例子

假设研究人员想要确定 20 个不同的变量是否与心脏病相关。他们一次执行 20 个单独的统计测试，并收到每个测试的 p 值。下表显示了每个测试的 p 值，按降序排列。

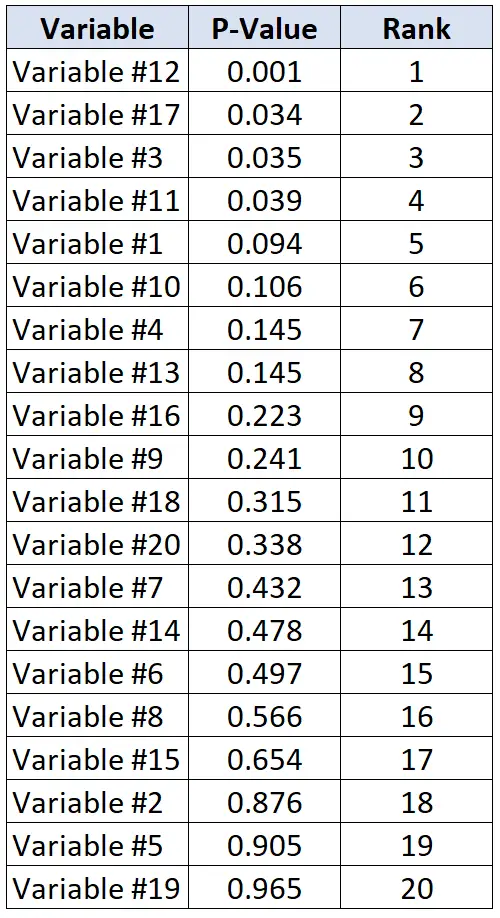
假设研究人员愿意接受 20% 的错误发现率。因此，要计算每个 p 值的临界 Benjamini-Hochberg 值，我们可以使用以下公式：(i/20)*0.2，其中i = p 值的排名。

下表显示了每个单独 p 值的临界 Benjamini-Hochberg 值：

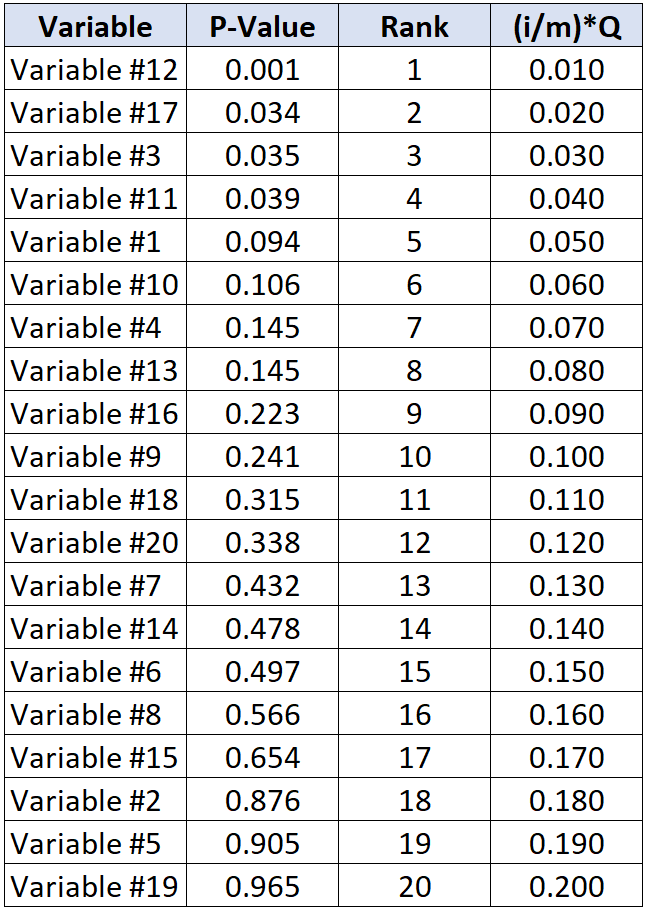
低于 Benjamini-Hochberg 临界值的最大 p 值的检验是变量 #11，其 p 值为 0.039，BH 临界值为 0.040。

因此，该检验和所有具有较小 p 值的检验将被视为显着。

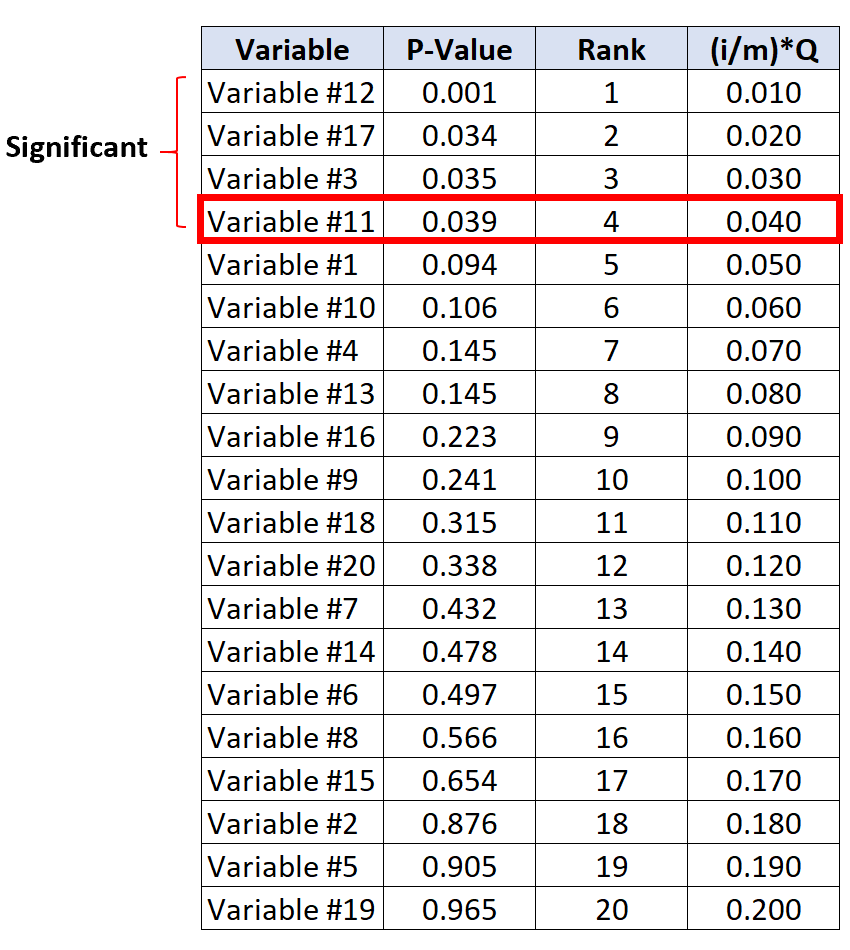
请注意，即使变量 #17 和 #3 的 p 值不小于其 BH 临界值，它们仍然被认为是显着的，因为它们的 p 值小于变量 #11。

如何选择错误发现率

本杰明-霍赫伯格程序中最重要的步骤之一是选择错误发现率。您应该在收集数据或执行统计测试之前选择错误发现率。

通常，您将在分析的探索阶段执行大量统计测试，然后进行其他测试以进一步探索结果。

如果后续测试成本低廉，那么您可能会考虑设置较高的错误发现率，因为即使您有一些错误发现，您也可能会在后续测试中发现这些错误发现。

此外，如果错过重要发现的成本很高，您可能需要提高错误发现率，以免错过任何重要的事情。

根据您的研究成本以及不错过任何重要发现的重要性，错误发现率会因情况而异。

其他资源

P值和统计显着性的解释
每个家庭的错误率是多少？