机器学习中什么是过度拟合？ （解释和示例）

在机器学习中，我们经常构建模型，以便能够对某些现象做出准确的预测。

例如，假设我们想要创建一个回归模型，使用预测变量学习时间来预测高中生响应变量的ACT 分数。

为了构建这个模型，我们将收集某个学区数百名学生的学习时间和相应的 ACT 分数数据。

然后，我们将使用这些数据来训练一个模型，该模型可以根据学习的总小时数来预测给定学生将获得的分数。

为了评估模型的有用性，我们可以衡量模型的预测与观察到的数据的匹配程度。执行此操作最常用的指标之一是均方误差 (MSE)，其计算如下：

MSE = (1/n)*Σ(y _i – f(x _i )) ²

金子：

• n：观察总数
• y _i ：^{第 i 个}观测值的响应值
• f( _xi ):第 i^个观测值的预测响应值

模型预测与观测值越接近，MSE 就越低。

然而，机器学习中犯的最大错误之一是优化模型以降低训练 MSE ，即模型预测与我们用于训练模型的数据的匹配程度。

当模型过于注重降低训练 MSE 时，它通常很难在训练数据中找到纯粹由偶然引起的模式。然后，当该模型应用于看不见的数据时，其性能很差。

这种现象称为过度拟合。当我们将模型“拟合”得太接近训练数据时，就会发生这种情况，从而最终构建一个对于新数据进行预测无用的模型。

过度拟合的示例

为了理解过度拟合，让我们回到创建回归模型的示例，该模型使用学习时间来预测ACT 分数。

假设我们收集某个学区 100 名学生的数据，并创建一个快速散点图来可视化两个变量之间的关系：

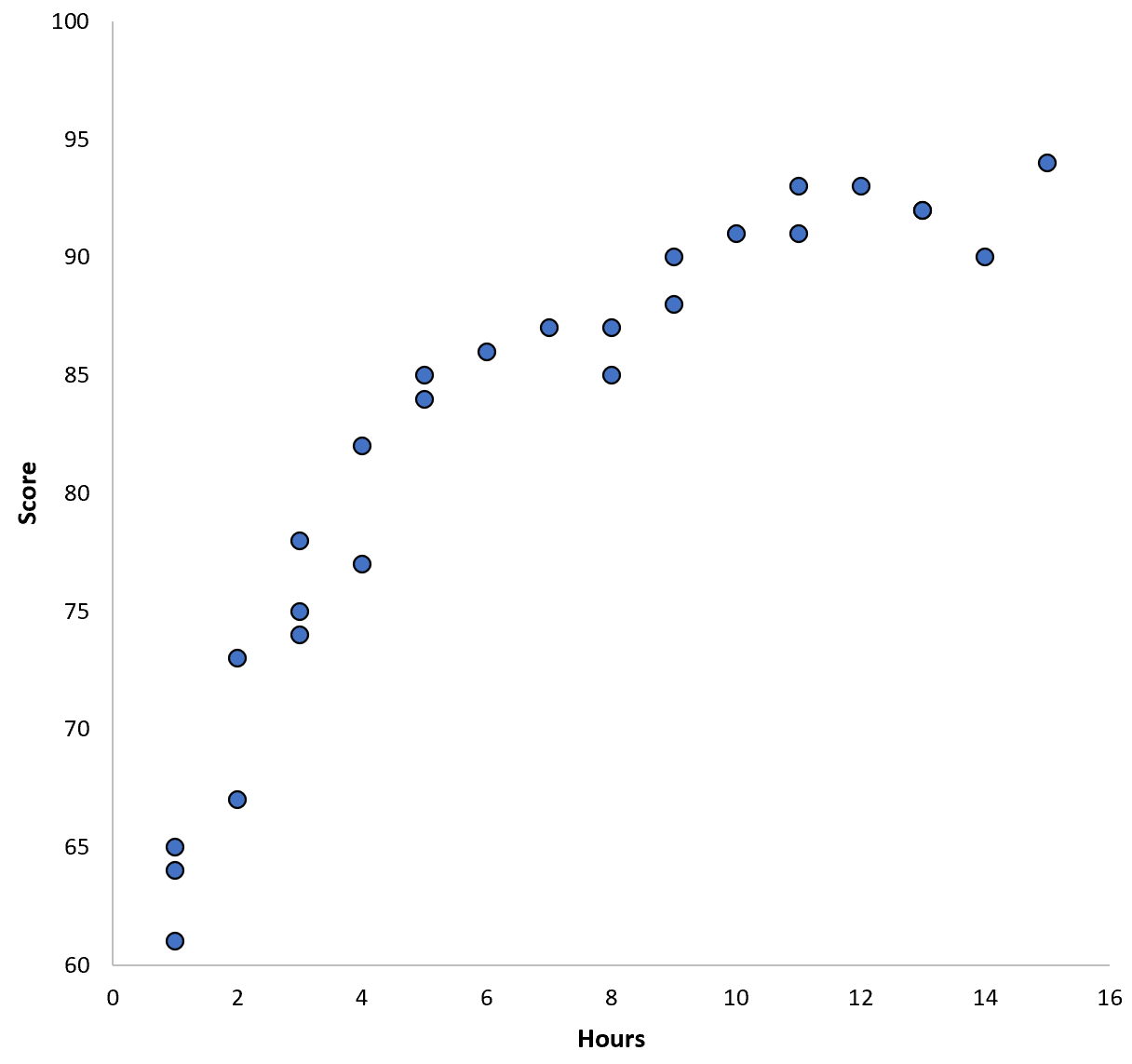
两个变量之间的关系似乎是二次关系，因此假设我们应用以下二次回归模型：

分数 = 60.1 + 5.4*(小时) – 0.2*(小时) ²

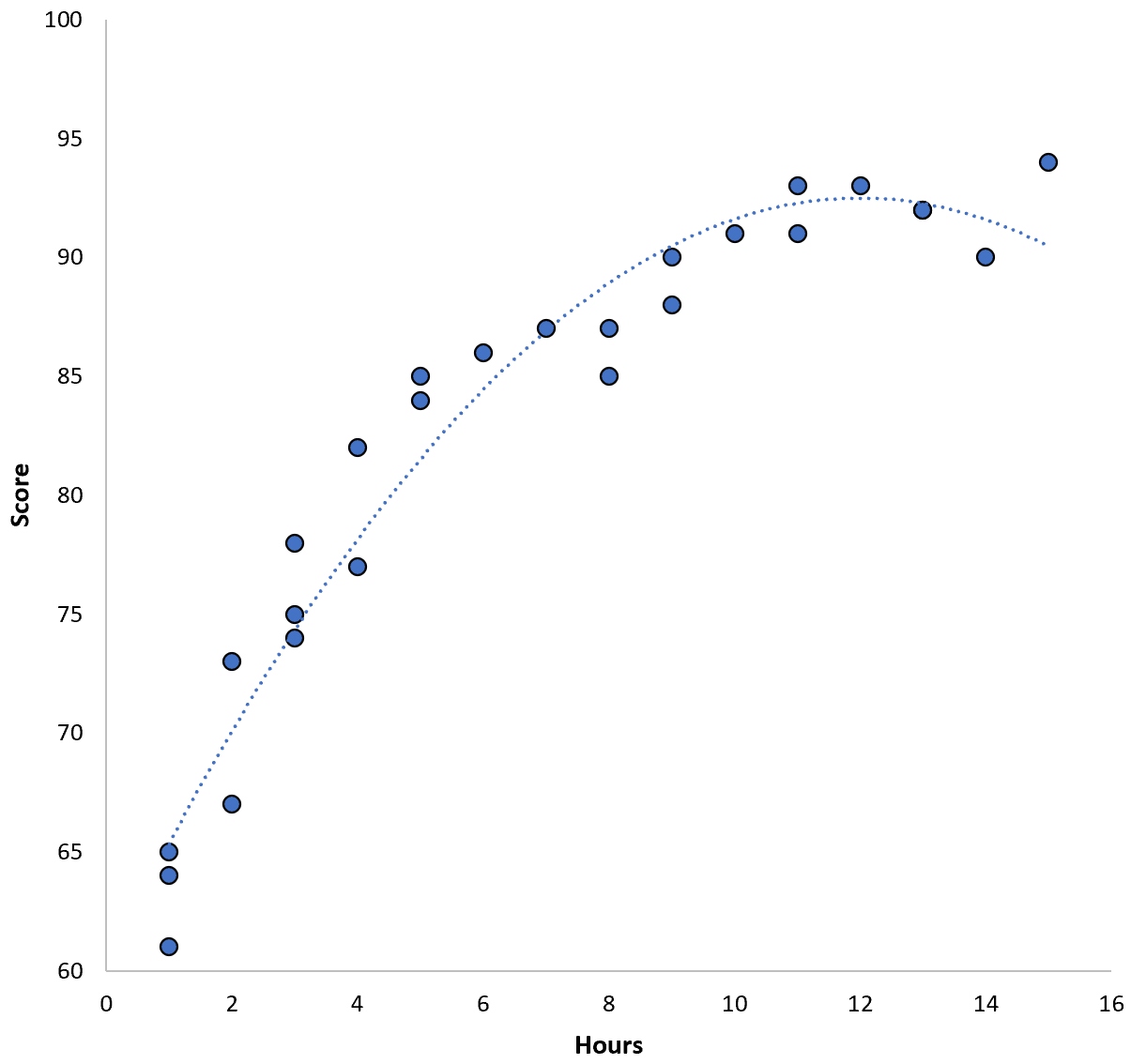
该模型的训练均方误差 (MSE) 为3.45 。也就是说，模型的预测与实际 ACT 分数之间的均方根差为 3.45。

然而，我们可以通过拟合高阶多项式模型来减少训练 MSE。例如，假设我们应用以下模型：

分数 = 64.3 – 7.1*(小时) + 8.1*(小时) ² – 2.1*(小时) ³ + 0.2*(小时^{) 4 – 0.1*(小时) 5 +} 0.2(小时) ⁶

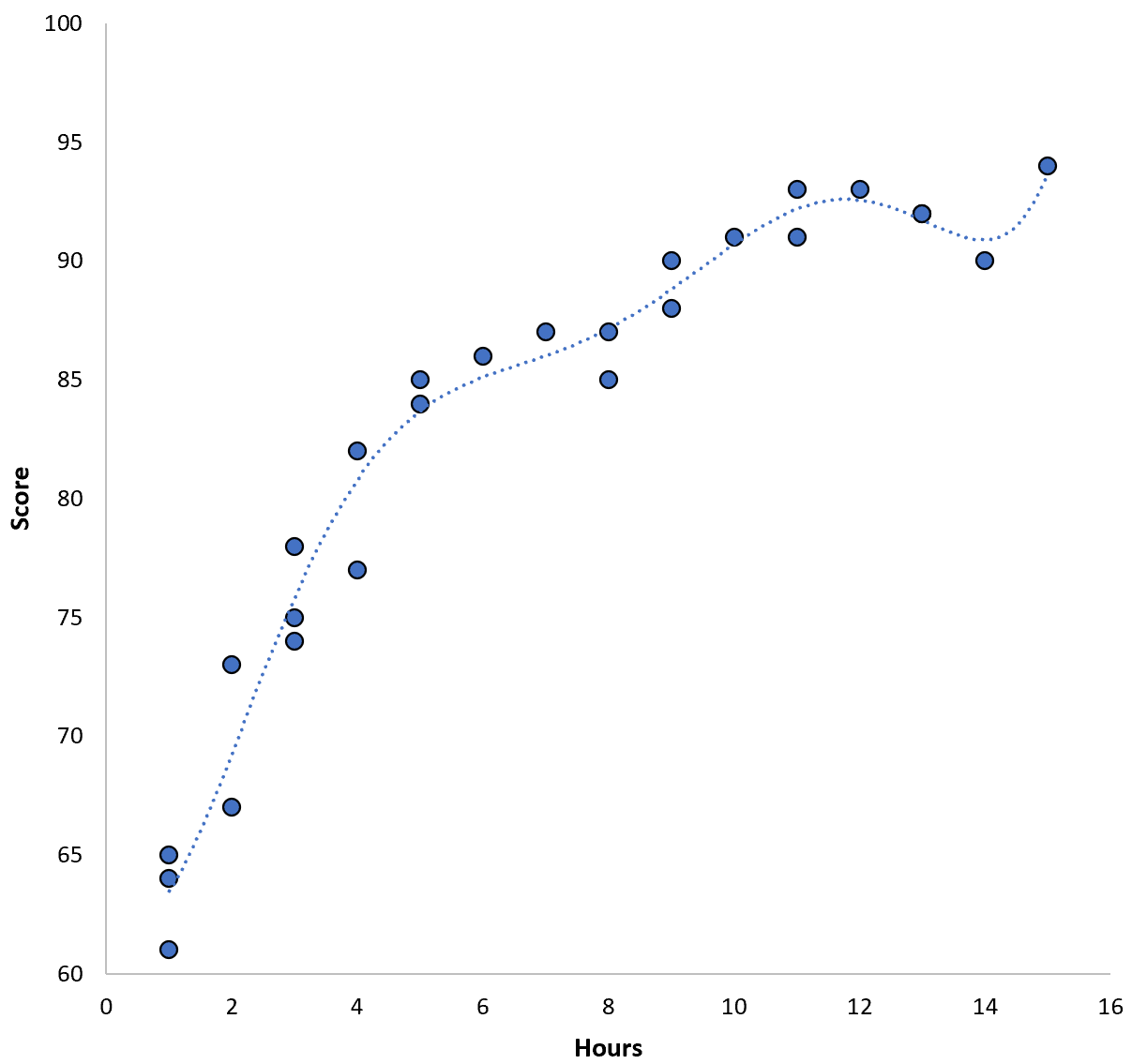
请注意回归线如何比之前的回归线更贴近实际数据。

该模型的训练均方根误差 (MSE) 仅0.89 。也就是说，模型的预测与实际 ACT 分数之间的均方根差为 0.89。

这个 MSE 训练比之前模型产生的训练要小得多。

然而，我们并不真正关心训练 MSE ，即模型的预测与我们用于训练模型的数据的匹配程度。相反，我们主要关心MSE 测试——当我们的模型应用于看不见的数据时的 MSE。

如果我们将上面的高阶多项式回归模型应用于看不见的数据集，它的性能可能会比更简单的二次回归模型更差。也就是说，它会产生更高的 MSE 测试，这正是我们不想要的。

如何检测并避免过度拟合

检测过度拟合的最简单方法是执行交叉验证。最常用的方法称为k 折交叉验证，其工作原理如下：

步骤 1：将数据集随机分为k组，或“折叠”，大小大致相等。

第 2 步：选择其中一个折叠作为您的固定集。将模板调整到剩余的 k-1 折叠。根据张紧层中的观测值计算 MSE 检验。

步骤 3：重复此过程k次，每次使用不同的集合作为排除集。

步骤 4：将测试的总体 MSE 计算为测试的k 个MSE 的平均值。

测试 MSE = (1/k)*ΣMSE _i

金子：

• k：折叠数
• MSE _i ：在^{第 i 次}迭代时测试 MSE

这个 MSE 测试让我们很好地了解给定模型在未知数据上的表现。

在实践中，我们可以拟合几个不同的模型，并对每个模型进行k折交叉验证，找出其MSE检验。然后，我们可以选择 MSE 测试最低的模型作为未来预测的最佳模型。

这确保我们选择一个可能在未来数据上表现最佳的模型，而不是简单地最小化训练 MSE 并“适合”历史数据的模型。

其他资源

机器学习中的偏差-方差权衡是什么？
K 折交叉验证简介
机器学习中的回归和分类模型