如何标准化 0 到 100 之间的数据
要将数据集中的值标准化在 0 到 100 之间,可以使用以下公式:
z i = (x i – 最小值 (x)) / (最大值 (x) – 最小值 (x)) * 100
金子:
- z i :数据集中的第 i 个归一化值
- x i :数据集的第 i 个值
- min(x) :数据集中的最小值
- max(x):数据集中的最大值
例如,假设我们有以下数据集:
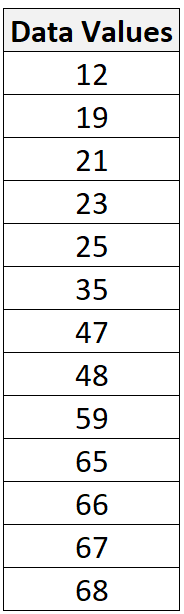
数据集中的最小值为 12,最大值为 68。
为了标准化12的第一个值,我们将应用之前共享的公式:
- z i = ( xi – 最小值(x)) / (最大值(x) – 最小值(x)) * 100 = (12 – 12) / (68 – 12) * 100 = 0
为了标准化19的第二个值,我们将使用相同的公式:
- z i = ( xi – 最小值(x)) / (最大值(x) – 最小值(x)) * 100 = (19 – 12) / (68 – 12) * 100 = 12.5
为了规范化21的第三个值,我们将使用相同的公式:
- z i = ( xi – 最小值(x)) / (最大值(x) – 最小值(x)) * 100 = (21 – 12) / (68 – 12) * 100 = 16.07
我们可以使用这个完全相同的公式将原始数据集中的每个值标准化为 0 到 100 之间:
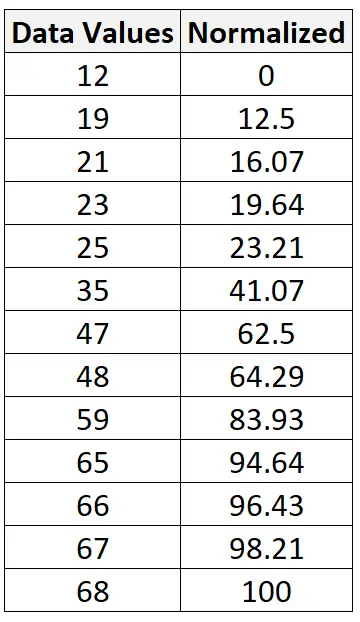
如何标准化任意范围之间的数据
我们实际上可以使用这个公式来标准化 0 到任意数字之间的数据集:
z i = (x i – 最小值 (x)) / (最大值 (x) – 最小值 (x)) * Q
其中Q是标准化数据值所需的最大数量。
在前面的示例中,我们选择 Q 为 100,但是通过选择 Q 为 1000,我们可以轻松标准化 0 到 1000 之间的数据值范围:
为了标准化12的第一个值,我们将应用以下公式:
- z i = ( xi – 最小值(x)) / (最大值(x) – 最小值(x)) * 1000 = (12 – 12) / (68 – 12) * 100 = 0
为了标准化19的第二个值,我们将使用相同的公式:
- z i = ( xi – 最小值(x)) / (最大值(x) – 最小值(x)) * 1000 = (19 – 12) / (68 – 12) * 100 = 125
为了规范化21的第三个值,我们将使用相同的公式:
- z i = ( xi – 最小值(x)) / (最大值(x) – 最小值(x)) * 1,000 = (21 – 12) / (68 – 12) * 100 = 160.7
我们可以使用这个完全相同的公式将原始数据集中的每个值标准化为 0 到 1000 之间:
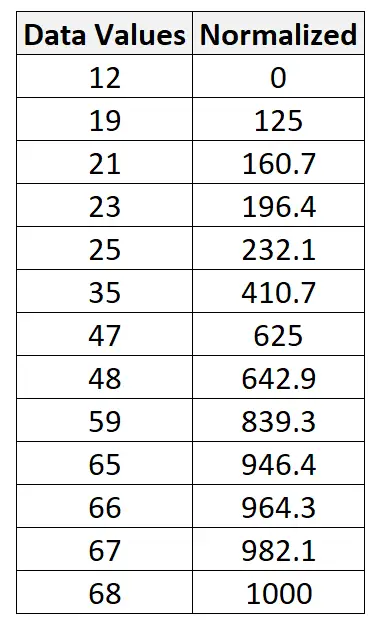
何时标准化数据
有时,当我们进行某种类型的分析时,我们会标准化变量,其中我们有多个在不同尺度上测量的变量,并且我们希望每个变量具有相同的范围。
这可以防止一个变量产生不适当的影响,特别是当它以不同的单位测量时(即,如果一个变量以英寸为单位,另一个以码为单位)。
还值得注意的是,我们在本教程中使用了一种称为最小-最大标准化的方法来标准化数据值。
两种最常见的标准化方法是:
1.最小-最大归一化
- 用途:将每个数据值转换为 0 到 100 之间的值。
- 公式:新值 = (值 – 最小值) / (最大值 – 最小值) * 100
2. 平均归一化
- 目的:缩放值,使所有值的平均值为 0 和 std。开发人员。是 1。
- 公式:新值=(值-平均值)/(标准差)
其他资源
如何标准化 0 到 1 之间的数据
如何在 Excel 中标准化数据
如何在 R 中标准化数据
如何在 Python 中规范化列