正态分布

经过本杰明·安德森博 8月 3, 2023 可能性 0 条评论

本文解释了统计学中的正态分布是什么。因此，您将找到正态分布的定义、正态分布的示例以及正态分布的属性。

什么是正态分布？

正态分布是一种连续概率分布，其图形呈钟形且关于其均值对称。在统计学中，正态分布用于对具有截然不同特征的现象进行建模，这就是该分布如此重要的原因。

事实上，在统计学中，正态分布被认为是迄今为止所有概率分布中最重要的分布，因为它不仅可以对大量现实世界的现象进行建模，而且正态分布还可以用来近似其他类型的概率分布。分布。在某些条件下。

正态分布的符号是大写字母N。因此，为了表示一个变量服从正态分布，用字母N表示，并在括号中添加其算术平均值和标准差的值。

$X\sim N(\mu,\sigma)$

正态分布有许多不同的名称，包括高斯分布、高斯分布和拉普拉斯高斯分布。

正态分布的例子

通常，遵循正态分布的数据集包含大量观察结果并涵盖非常普遍的主题。以下是通常可以用正态分布建模的统计样本的几个示例。

正态分布的示例：

课程中的学生人数。
公司员工的智商。
工厂一天生产的缺陷零件数量。
学生在课程考试中获得的成绩。
在证券交易所上市公司股票的盈利能力。

正态分布图

一旦我们了解了什么是正态分布以及此类概率分布的一些示例，让我们看看它的图形是什么样的，以便更好地理解这个概念。

在下图中，您可以看到正态分布的密度函数如何根据其算术平均值和标准差的值而变化。

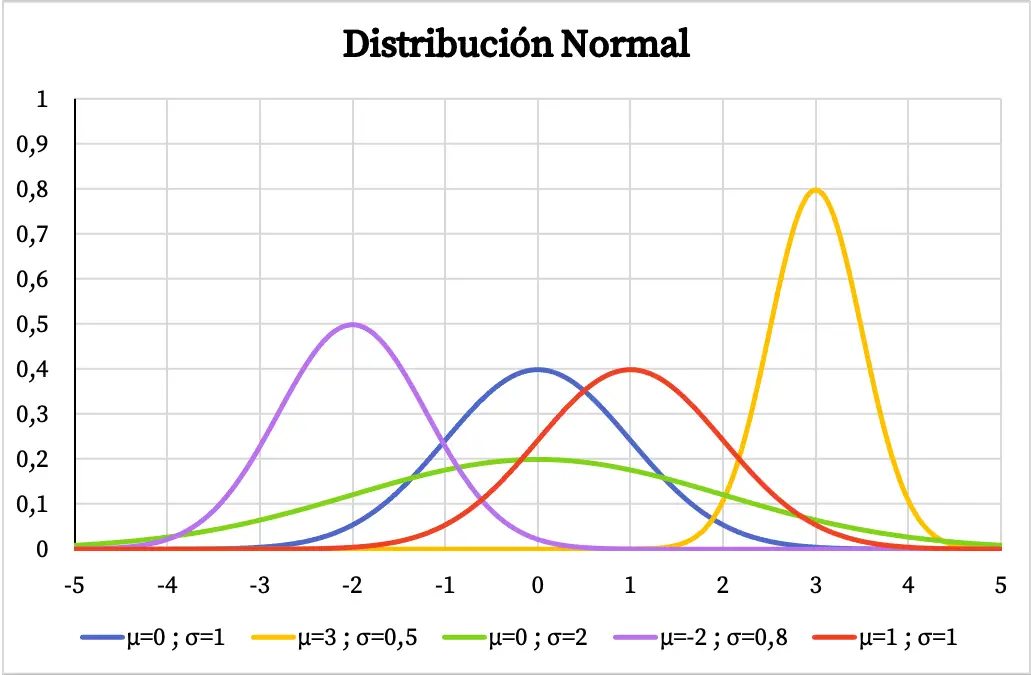
具有以算术平均值为中心的钟形形状，如果变量具有正态分布，则意味着重复次数最多的值是平均值，并且平均值周围的值比极值重复的频率更高。同样，正态分布的标准差越大，其图形表示的形状越平坦。

另一方面，正态分布的累积概率函数的图形也取决于其算术平均值和标准差的值，如下图所示：

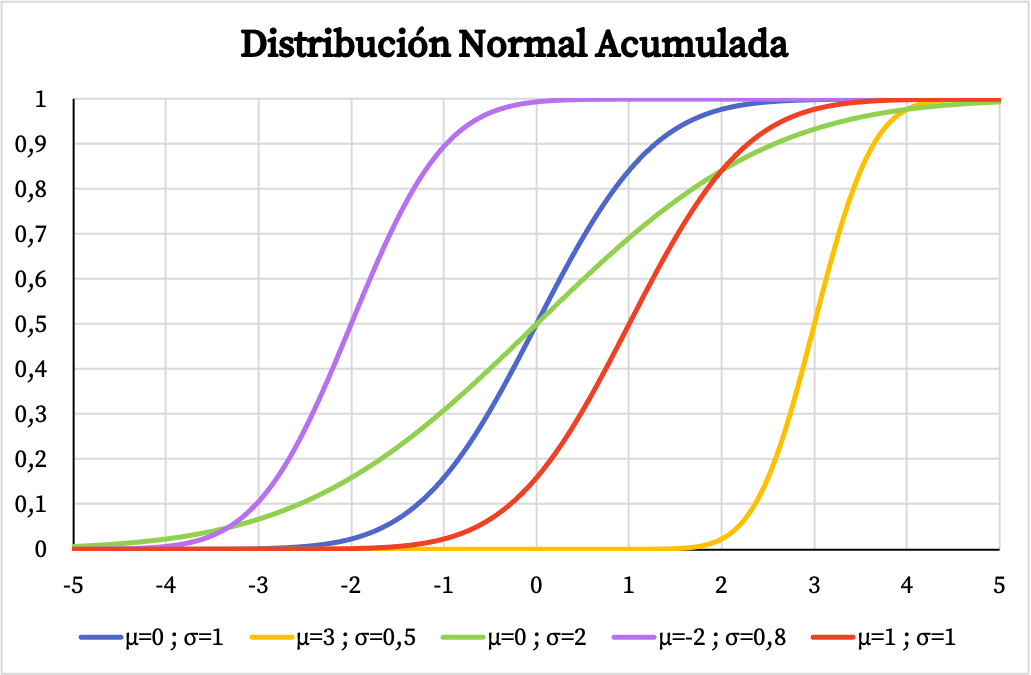
正态分布的密度函数和分布函数使得计算与该分布相关的概率成为可能。但是，您可以直接使用正态分布表，而不是使用它们的公式，因为它更快。您可以通过以下链接查阅这些表格：

➤参见：正态分布表

正态分布的特征

正态分布具有以下特点：

正态分布取决于两个特征参数，即算术平均值 (μ) 和标准差 (σ)。

$X\sim N(\mu,\sigma)$

正态分布可以取正值和负值，因此正态分布的域由实数组成。

$x\in \mathbb{R}$

正态分布的中位数和众数等于分布的算术平均值。

$Me=Mo=\mu$

正态分布的偏度系数和峰度系数为零。

$\begin{array}{c}A=0\\[2ex]C=0\end{array}$

正态分布的密度函数的公式为：

$\displaystyle P[X=x]=\frac1{\sigma\sqrt{2\pi}}\; e^{ - \frac{(x-\mu)^2}{2\sigma^2}}$

类似地，正态分布的累积概率函数的公式为：

$\displaystyle P[X\leq x]=\frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^x e^{-\frac{(x - \mu)^2}{2\sigma^2}}\, dx ,\quad x\in\mathbb{R}$

中心极限定理的一个应用是，当 λ 值足够大时，泊松分布可以近似正态分布。

$\text{Poisson}(\lambda)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(\lambda, \sqrt{\lambda}\right)$

中心极限定理的另一个应用是，对于具有大量观测值的数据集，二项式分布可以通过正态分布来近似。

$\text{Bin}(n,p)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(n\cdot p, \sqrt{n\cdot p \cdot (1-p)}\right)$

标准正态分布

标准正态分布，也称为单位正态分布，是正态分布的最简单情况。更准确地说，标准正态分布是均值和标准差值分别等于0和1的正态分布。

$\displaystyle N(0,1) \ \color{orange}\bm{\longrightarrow}\color{black}\begin{cases} \mu=0\\[2ex]\sigma=1\end{cases}$

请注意，任何正态分布都可以通过应用称为打字的过程转换为标准正态分布，该过程包括从每个值中减去其算术平均值，然后除以其标准差。

此外，标准正态分布用于使用其概率表来确定正态分布的任何概率。因此，为了找到正态分布的概率，首先输入变量将其转换为标准正态分布，然后我们在表中查看相应的概率值是多少。要了解更多信息，请单击以下链接：

➤请参阅：标准正态分布

正态分布和经验规则

在统计学中，经验法则，也称为68-95-99.7 规则，是定义正态分布中落在平均值的三个标准差范围内的值的百分比的规则。

更具体地说，经验法则如下：

正态分布中 68% 的值位于平均值的一个标准差之内。
正态分布中 95% 的值位于平均值的两个标准差之内。
正态分布中 99.7% 的值落在平均值的三个标准差范围内。

关于作者

本杰明·安德森博

大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多