正态分布
正态分布是统计学中最常见的概率分布。

正态分布具有以下特征:
- 钟形
- 对称
- 平均值和中位数相等;两者都位于分布的中心
- 大约 68% 的数据落在平均值的一个标准差范围内
- 大约 95% 的数据落在平均值的两个标准差之内。
- 大约 99.7% 的数据落在平均值的三个标准差范围内。
最后三点被称为经验法则,有时也称为68-95-99.7 法则。
相关:经验法则(实践问题)
如何绘制正态曲线
要绘制正态曲线,我们需要知道平均值和标准差。
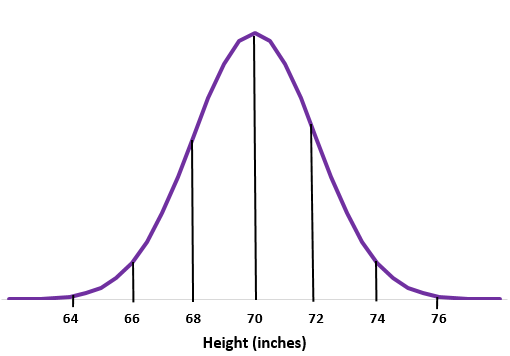
示例 1:假设某所学校的男生身高服从正态分布,平均值为标准差为
步骤一:画一条法线。
步骤2:70英寸的平均值在中间。
步骤 3:每个标准偏差对应 2 英寸的距离。
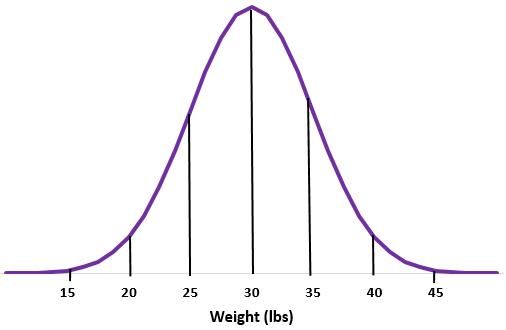
示例 2:假设某种水獭的重量服从正态分布,平均值为标准差为
步骤一:画一条法线。
第 2 步: 30 磅的平均值落在中间。
步骤 3:每个标准差对应 5 磅的距离
如何使用正态分布求百分比
经验法则(有时称为68-95-99.7 规则)指出,对于正态分布的随机变量,68% 的数据落在与平均值相差一个标准差的范围内,95% 落在与平均值相差两个标准差的范围内与平均值的偏差 99.7% 在平均值的三个标准差以内。

使用这个规则我们可以回答有关百分比的问题。
示例:假设某所学校的男生身高呈正态分布,平均值为标准差为
解决方案:
步骤 1:绘制平均值为标准差为
第 2 步: 74 英寸的高度比平均值高出两个标准差。将高于该点的百分比添加到正态分布中。
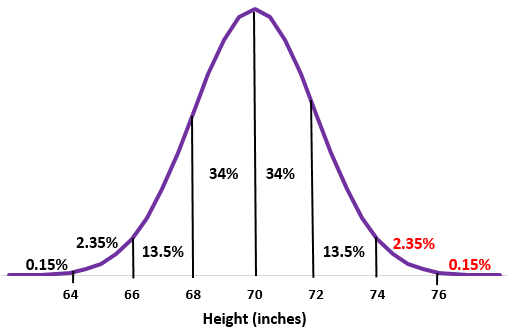
2.35% + 0.15% = 2.5%
这所学校大约2.5%的男生身高超过 74 英寸。
解决方案:
步骤 1:绘制平均值为标准差为
第 2 步: 68 英寸和 72 英寸的高度分别比平均值低一个标准差和比平均值高一个标准差。只需将正态分布中这两点之间的百分比相加即可。
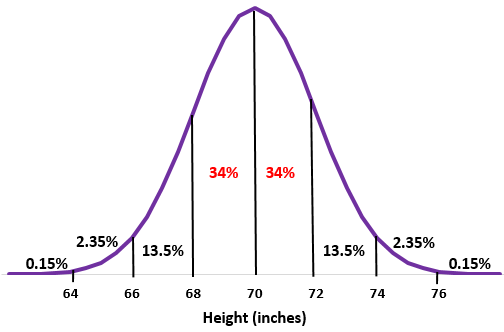
34% + 34% = 68%
这所学校大约68%的男生身高在 68 英寸到 72 英寸之间。
如何使用正态分布查找计数
我们还可以使用经验法则来回答有关计数的问题。
示例:假设某种水獭的重量服从正态分布,平均值为标准差为
某个群体有 200 只这样的水獭。这些水獭中大约有多少重量超过 35 磅?
解决方案:
步骤 1:绘制平均值为标准差为的正态分布。
第 2 步: 35 磅的重量比平均值高一个标准差。将高于该点的百分比添加到正态分布中。
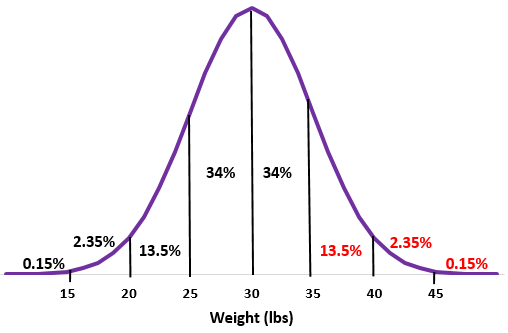
13.5% + 2.35% + 0.15% = 16%
步骤 3:由于群体中有 200 只水獭,200 只的 16% = 0.16 * 200 = 32
这个群体中约有 32 只水獭体重超过 35 磅。
这个群体中大约有多少只水獭体重低于 30 磅?
我们可以认识到正态分布的中位数等于均值,在本例中为 30 磅,而不是遵循我们上面刚刚执行的所有步骤。
这意味着一半的水獭体重超过30磅,另一半的体重低于30磅。这意味着 200 只水獭中有 50% 的体重小于 30 磅,因此 0.5 * 200 = 100 只水獭。
其他资源
以下教程提供有关正态分布的其他信息:
正态分布的 6 个具体例子
正态分布与 t 分布:差异
如何在 Excel 中创建钟形曲线
如何用 Python 创建钟形曲线