如何在 stata 中测试正态性
许多统计测试要求一个或多个变量服从正态分布,测试结果才可靠。
本教程介绍了可用于测试 Stata 中变量之间的正态性的几种方法。
对于每种方法,我们将使用名为auto的内置 Stata 数据集。您可以使用以下命令加载此数据集:
系统自动使用
方法一:直方图
查看变量是否服从正态分布的一种非正式方法是创建直方图来显示变量的分布。
如果变量呈正态分布,则直方图应呈“钟形”形状,靠近中心的值较多,位于尾部的值较少。
我们可以使用hist命令为变量位移创建直方图:
感动的历史
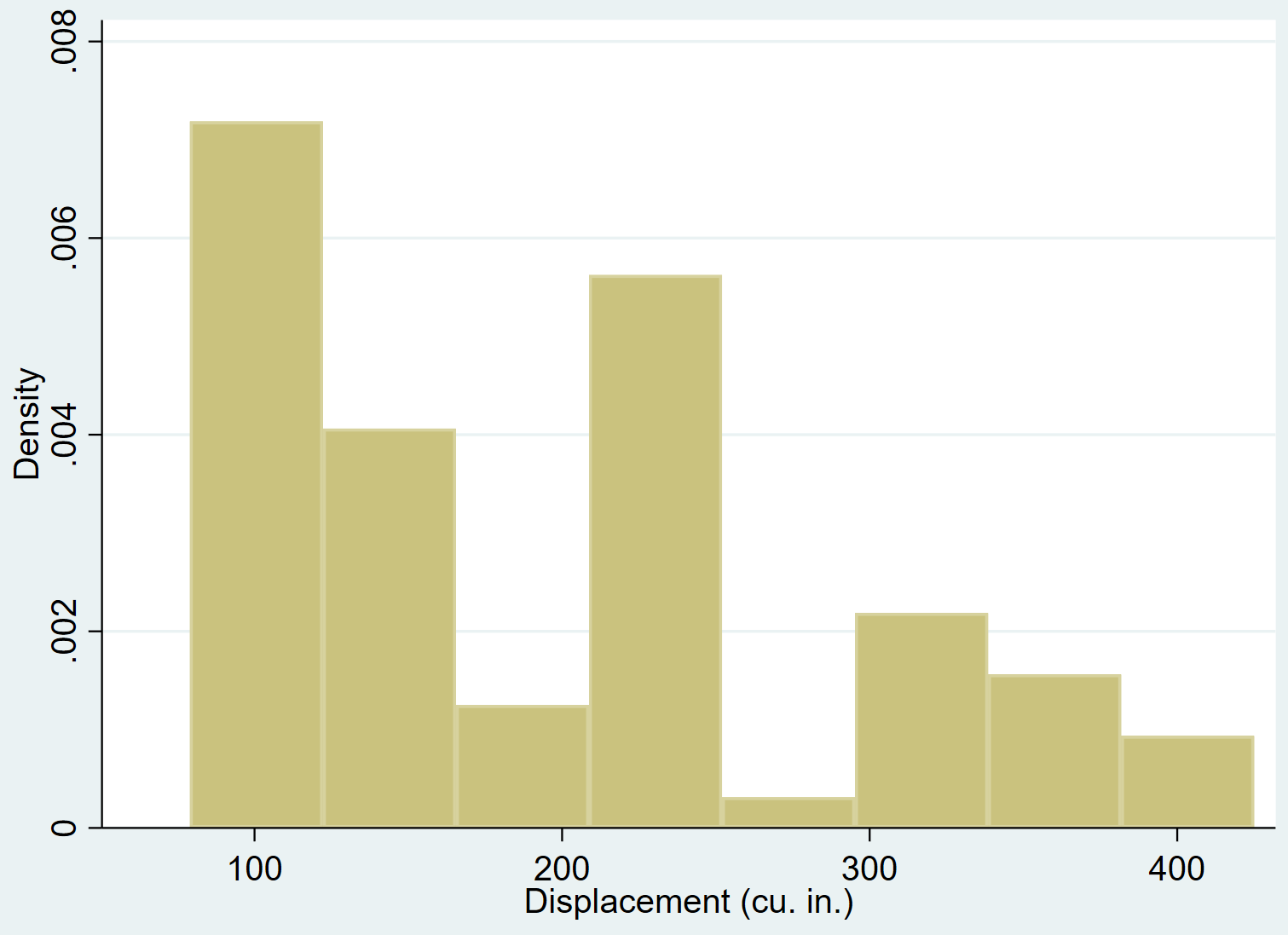
我们可以使用法线命令将正态密度曲线添加到直方图:
搬家史,正常
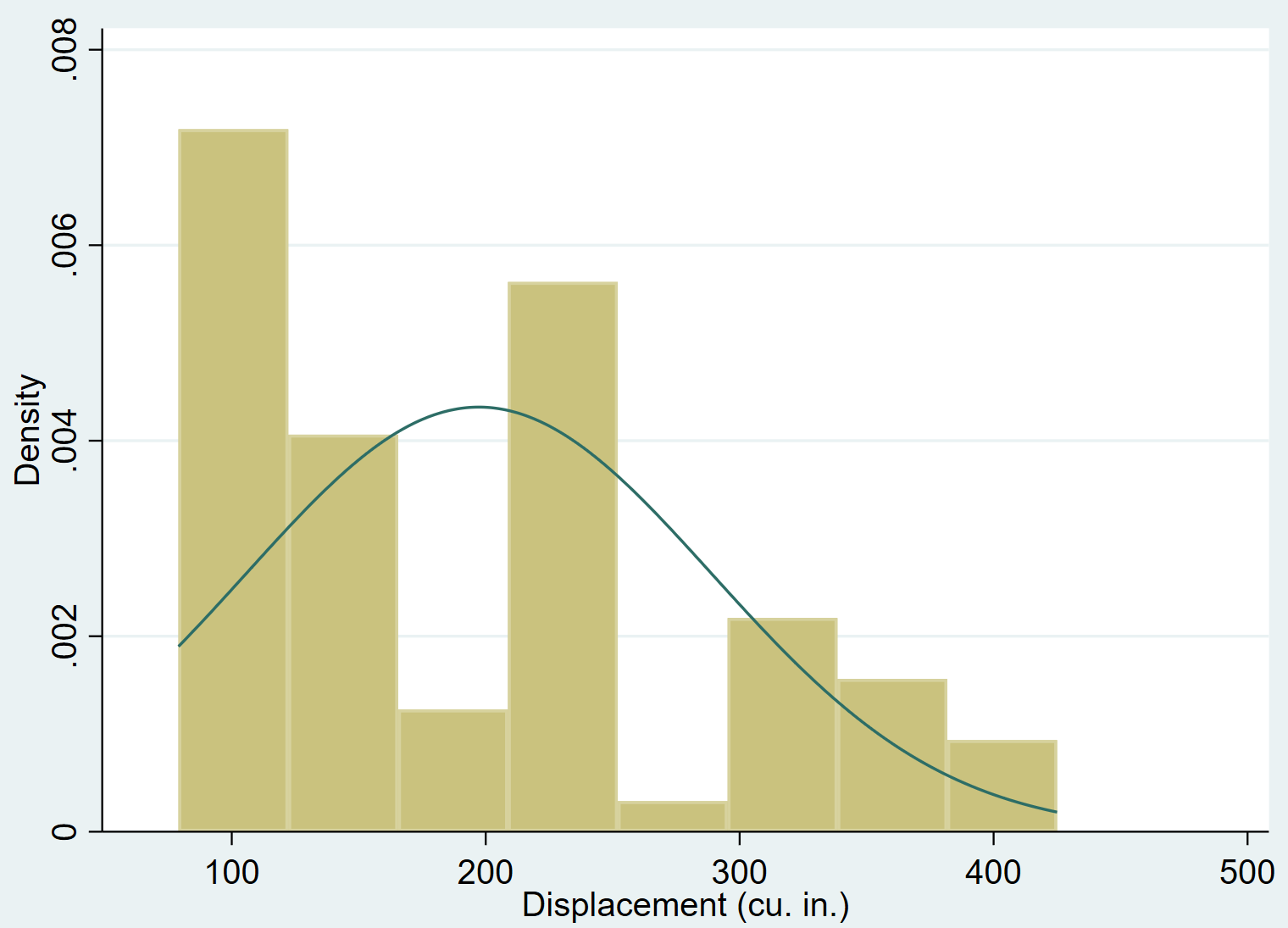
很明显,变量移位向右倾斜(例如,大多数值集中在左侧,并且值的长“尾巴”延伸到右侧)并且不遵循正态分布。
相关:左偏态分布和右偏态分布
方法 2:夏皮罗-威尔克检验
检验正态性的一种正式方法是使用Shapiro-Wilk 检验。
此检验的原假设是变量呈正态分布。如果检验的p 值低于一定的显着性水平(常见选择包括 0.01、0.05 和 0.10),那么我们可以拒绝零假设并得出结论:有足够的证据断言变量不呈正态分布。
*当观察总数在 4 到 2,000 之间时可以使用此检验。
我们可以使用swilk命令对变量位移执行 Shapiro-Wilk 检验:
平稳运动

以下是如何解释测试结果:
观测值:74。这是测试中使用的观测值数量。
宽:0.92542。这是测试的测试统计量。
概率>z:0.00031。这是与检验统计量相关的 p 值。
由于 p 值小于 0.05,我们可以拒绝检验的原假设。我们有足够的证据表明可变位移不是正态分布的。
我们还可以通过在swilk命令后列出多个变量来同时对多个变量执行 Shapiro-Wilk 检验:
swalk 排量 mpg 长度
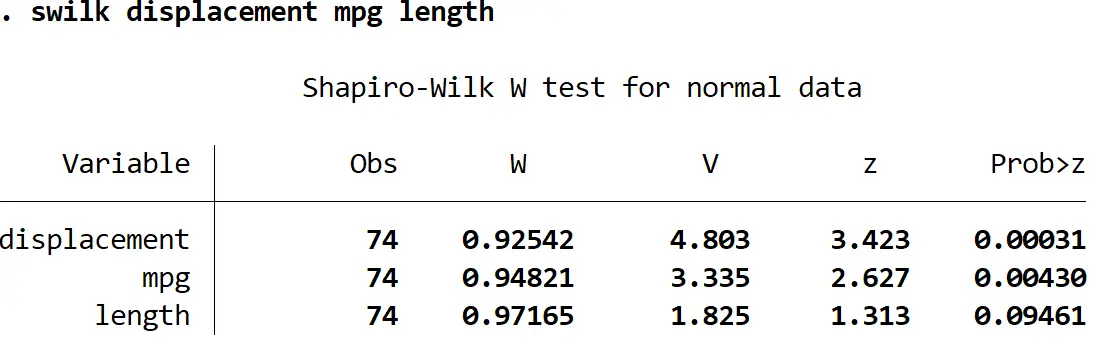
使用 0.05 的显着性水平,我们可以得出结论,位移和mpg不是正态分布的,但我们没有足够的证据表明长度不是正态分布的。
方法 3:Shapiro-Francia 检验
检验正态性的另一种正式方法是使用Shapiro-Francia 检验。
此检验的原假设是变量呈正态分布。如果检验的 p 值低于一定的显着性水平,那么我们可以拒绝原假设并得出结论:有足够的证据表明该变量不是正态分布的。
*当观察总数在 10 到 5,000 之间时可以使用此检验。
我们可以使用sfrancia命令对变量位移执行 Shapiro-Wilk 检验:
移动法兰西亚

以下是如何解释测试结果:
观测值:74。这是测试中使用的观测值数量。
W’:0.93011。这是测试的测试统计量。
概率>z:0.00094。这是与检验统计量相关的 p 值。
由于 p 值小于 0.05,我们可以拒绝检验的原假设。我们有足够的证据表明可变位移不是正态分布的。
与 Shapiro-Wilk 检验类似,您可以通过在sfrancia命令后列出多个变量来一次对多个变量执行 Shapiro-Francia 检验。
方法4:偏度和峰度测试
检验正态性的另一种方法是使用偏度和峰度检验,它确定变量的偏度和峰度是否符合正态分布。
此检验的原假设是变量呈正态分布。如果检验的 p 值低于一定的显着性水平,那么我们可以拒绝原假设并得出结论:有足够的证据表明该变量不是正态分布的。
*此测试需要至少使用 8 个观察值。
我们可以使用sktest命令对变量位移进行偏度和峰度测试:
移动测试

以下是如何解释测试结果:
观测值:74。这是测试中使用的观测值数量。
形容词气(2):5.81。这是检验的卡方检验统计量。
概率>chi2:0.0547。这是与检验统计量相关的 p 值。
由于 p 值不小于 0.05,因此我们无法拒绝检验的原假设。我们没有足够的证据表明运动不是正态分布的。
与其他正态性检验类似,您可以通过在sktest命令后列出多个变量来一次对多个变量执行偏度和峰度检验。