标准正态分布

本文解释什么是标准正态分布以及它的用途。您还将找到标准正态分布的属性、及其特征值的表格，以及已解决的练习。

什么是标准正态分布？

标准正态分布，也称为单位正态分布，是正态分布的最简单情况。更准确地说，标准正态分布是均值和标准差值分别等于0和1的正态分布。

因此，标准正态分布定义为 N(0,1)，其中第一个参数是分布的平均值，第二个参数是其标准差（或 SD）。

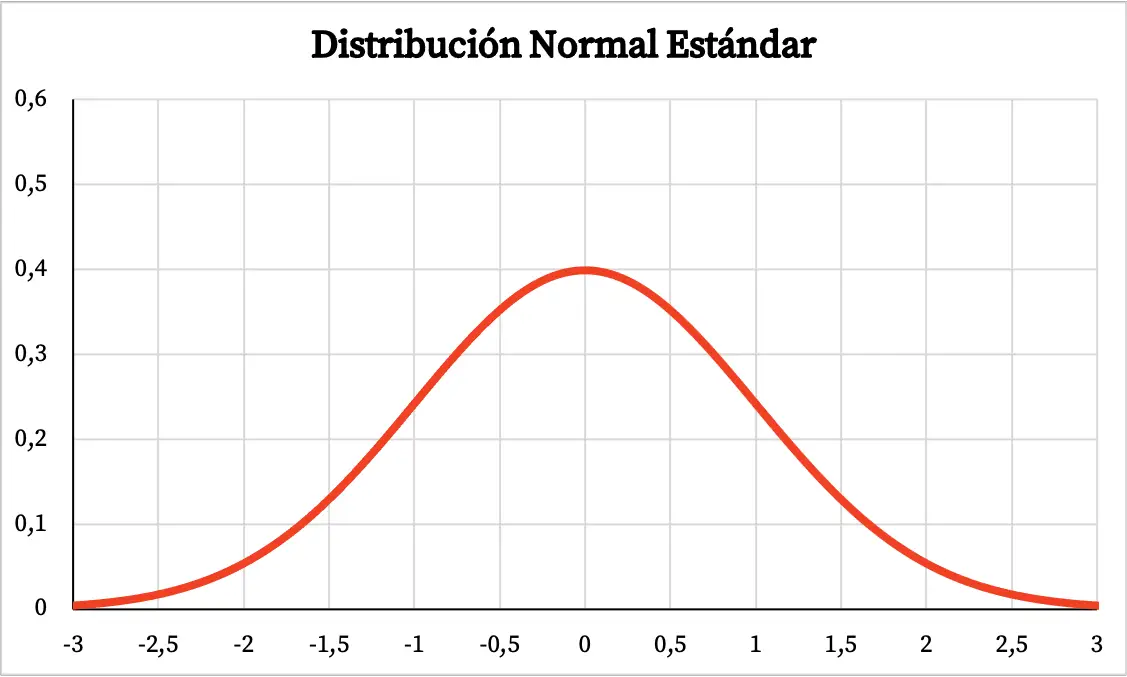
因此，标准正态分布图如下：

标准正态分布的公式

要将任何正态分布转换为标准正态分布，必须从其所有值中减去正态分布的均值，然后除以正态分布的标准差。

因此，标准正态分布的公式如下：

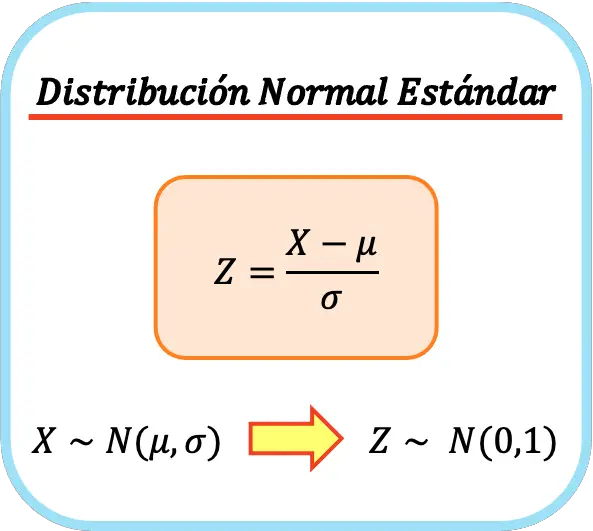
这样，新变量的算术平均值和标准差将分别为0和1，这样我们就得到了标准正态分布。这个过程也称为单变量归一化或单变量归一化。

标准正态分布表

标准正态分布表是包含观测值小于标准正态分布给定值的概率的表。

此外，由于正态分布的函数取决于其均值和标准差，因此扩展后还可以使用标准正态分布表来确定任何正态分布的概率。为此，将正态分布输入标准正态分布，然后我们在表中查看与其对应的概率。

那么，标准正态分布表中的数值如下：

标准正态分布示例

现在我们知道了标准正态分布的定义及其公式是什么，下面是一个具体的例子来更好地理解这个概念。

• 连续随机变量服从均值 45、标准差 15 的正态分布，获得小于或等于 58 的值的概率是多少？

为了找到正态分布的概率，我们需要使用它的特征表，但要做到这一点，我们首先需要进行输入过程以获得标准正态分布。因此，我们使用标准正态分布公式：

所以我们从概率值中减去平均值，然后除以标准差

一旦我们对变量进行了标准化，我们就可以转到标准正态分布概率表（见上文）来查看 0.87 的值对应的概率是多少：

因此，获得等于或小于 58 的值的概率为 80.78%。

标准正态分布的特征

标准正态分布具有以下特点：

• 标准正态分布是以 0 为中心的对称分布。
• 与正态分布一样，标准正态分布图是钟形的，大部分图形区域落在平均值附近。
• 因此，正态分布的均值、众数和中位数具有相同的值，均为 0。
• 标准正态分布在 z=0 处有最大值。
• 类似地，标准正态分布有两个拐点，分别位于 z=-1 和 z=+1 处。
• 根据经验法则，我们知道 68% 的值落在 +1 和 -1 之间的标准正态分布，95% 的值落在 +2 和 -2 之间，99.7% 的值落在 + 之间3和-3。