正相关
在本文中,您将了解正相关在统计学中的含义、正相关变量的示例以及其他类型相关性之间的差异。
什么是正相关?
在统计学中,正相关是两个不同变量之间的一种相关性。更具体地说,两个变量之间的正相关意味着如果一个变量的值增加,另一个变量也会增加。
为了使两个变量之间的相关性被视为正相关,相关系数的值必须介于 0(不包括在内)和 1(包括在内)之间。
请注意,正相关也可以称为直接相关。
正相关示例
考虑到正相关的定义,下面是表现出这种相关性的两个变量的示例。
- 在下面的频数表中,收集了 20 名学生的数学和统计成绩作为数据。分析两个变量之间的关系。
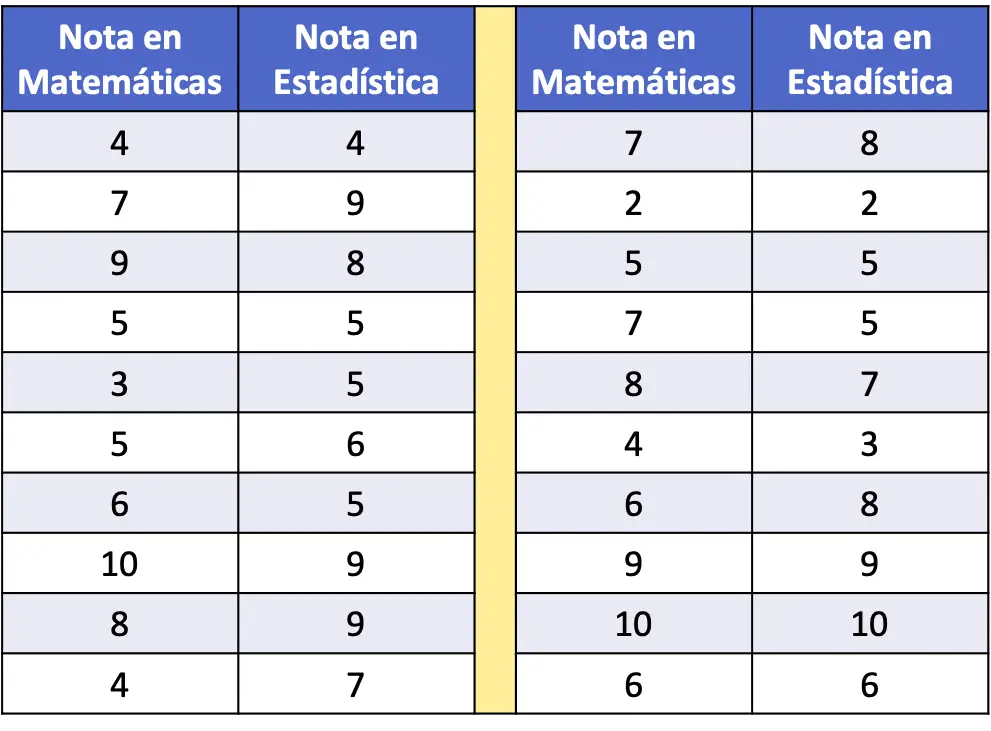
在计算相关系数之前,建议首先将统计数据集以散点图表示,以进行初步探索。
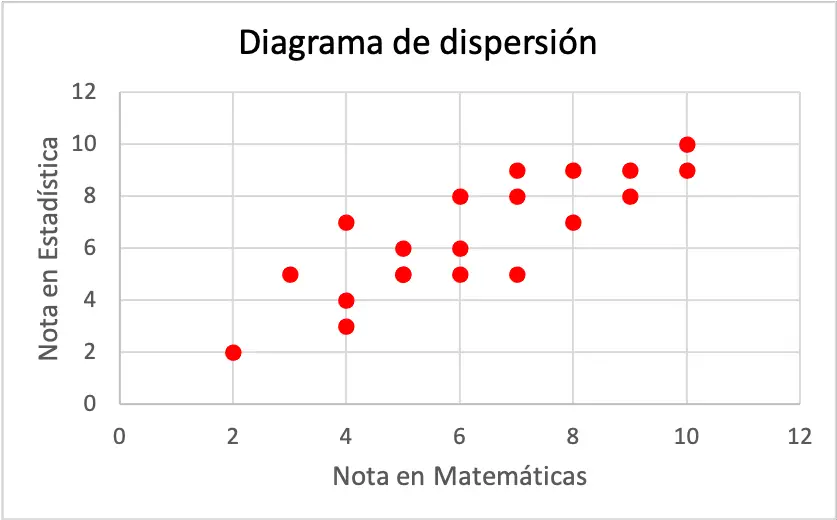
如图所示,这两个变量似乎具有正线性相关性,因为随着数学成绩的提高,统计成绩也会提高。但为了确定相关性的类型,有必要计算相关系数:
![]()
皮尔逊相关系数的值大于 0 并且非常接近 1,因此研究的两个变量之间的相关性确实是正相关。
正相关的解释
为了理解统计中正相关的含义,我们将在本节中了解如何解释两个变量之间的正相关值。
相关系数的值越高,两个变量的正相关程度就越大。因此,当相关系数的值接近1时,意味着两个变量之间的相关性是正的并且非常强。
另一方面,当相关系数的值较低且接近于零时,这意味着两个变量之间的相关性为正但较弱。即使相关系数变为零或负,这也分别意味着相关性为零或负。下面我们将看到这三种相关性之间的差异。
最后,应该注意的是,正相关并不意味着变量之间存在因果关系。也就是说,如果两个变量存在正相关,则意味着它们是线性相关的,但一个变量不一定是另一个变量的原因。
与上一节类似,数学和统计学的成绩是正相关的,但是数学成绩好并不能自动保证统计学成绩好,而是必须学习这两门科目。总之,数学成绩并不是统计学成绩的原因,这两个变量是简单相关的。
正相关、负相关和零相关
除了正相关之外,在统计中,两个变量还可以具有负相关或零相关。因此,在本节中我们将了解如何区分这三种类型的相关性。
- 正相关:当一个变量增加时,另一个变量也增加。相关系数的值在0(不含)和1(含)之间。
- 负相关:当一个变量增加时,另一个变量减少,反之亦然,如果一个变量减少,另一个变量增加。相关系数的值在-1(含)和0(不含)之间。
- 零相关:两个变量之间没有关系。相关系数等于 0。
在下面的图表中,您可以看到所代表的每种类型的相关性:
