剩余间隙是多少? (定义&;示例)
残差方差(有时称为“无法解释的方差”)是指模型中无法用模型变量解释的方差。
模型的残差方差越高,模型解释数据变化的能力就越弱。
残差出现在两种不同统计模型的结果中:
1. 方差分析:用于比较三个或更多独立组的均值。
2.回归:用于量化一个或多个预测变量与响应变量之间的关系。
以下示例展示了如何解释每种方法中的残差方差。
方差分析模型中的残差方差
每次我们拟合 ANOVA(“方差分析”)模型时,我们最终都会得到如下所示的 ANOVA 表:
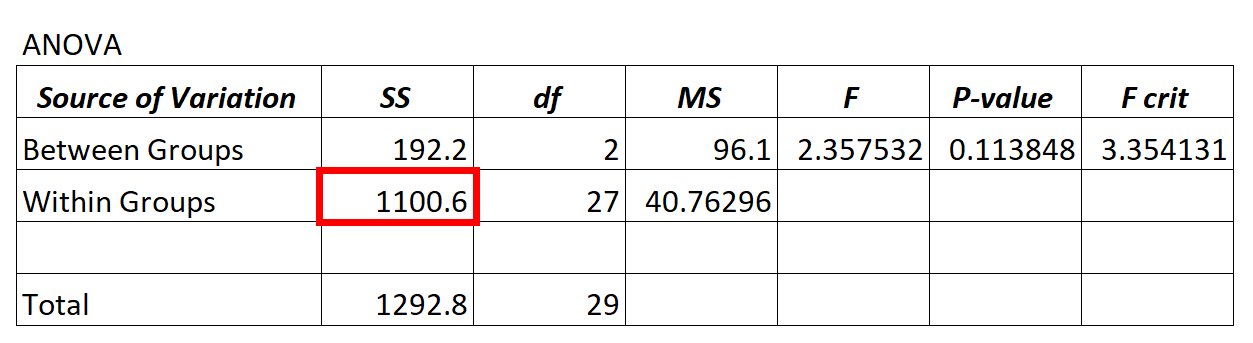
ANOVA 模型的残差方差值可在组内变异的 SS(“平方和”)列中找到。
该值也称为“误差平方和”,使用以下公式计算:
Σ(X ij – X j ) 2
金子:
- Σ :希腊符号,意思是“和”
- X ij : j 组的第 i 个观察值
- X j : 第 j 组的平均值
在上面的方差分析模型中,我们看到残差方差为 1100.6。
为了确定残差方差是否“高”,我们可以计算组内的平均平方和和组间的平均平方和,并找到两者之间的比率,从而给出方差分析表中的总体 F 值。
- F = MS进入/ MS进入
- F = 96.1 / 40.76296
- F = 2.357
上面ANOVA表中的F值为2.357,对应的p值为0.113848。由于该 p 值不小于 α = 0.05,因此我们没有足够的证据来拒绝原假设。
这意味着我们没有足够的证据表明我们所比较的组之间的平均差异存在显着差异。
这告诉我们,方差分析模型的残差方差比模型实际可以解释的方差要高。
回归模型中的残差方差
在回归模型中,残差方差定义为预测数据点与观测数据点之间差异的平方和。
计算方法如下:
Σ(ŷ i – y i ) 2
金子:
- Σ :希腊符号,意思是“和”
- ŷ i :预测的数据点
- y i :观察到的数据点
当我们拟合回归模型时,我们通常会得到如下所示的结果:
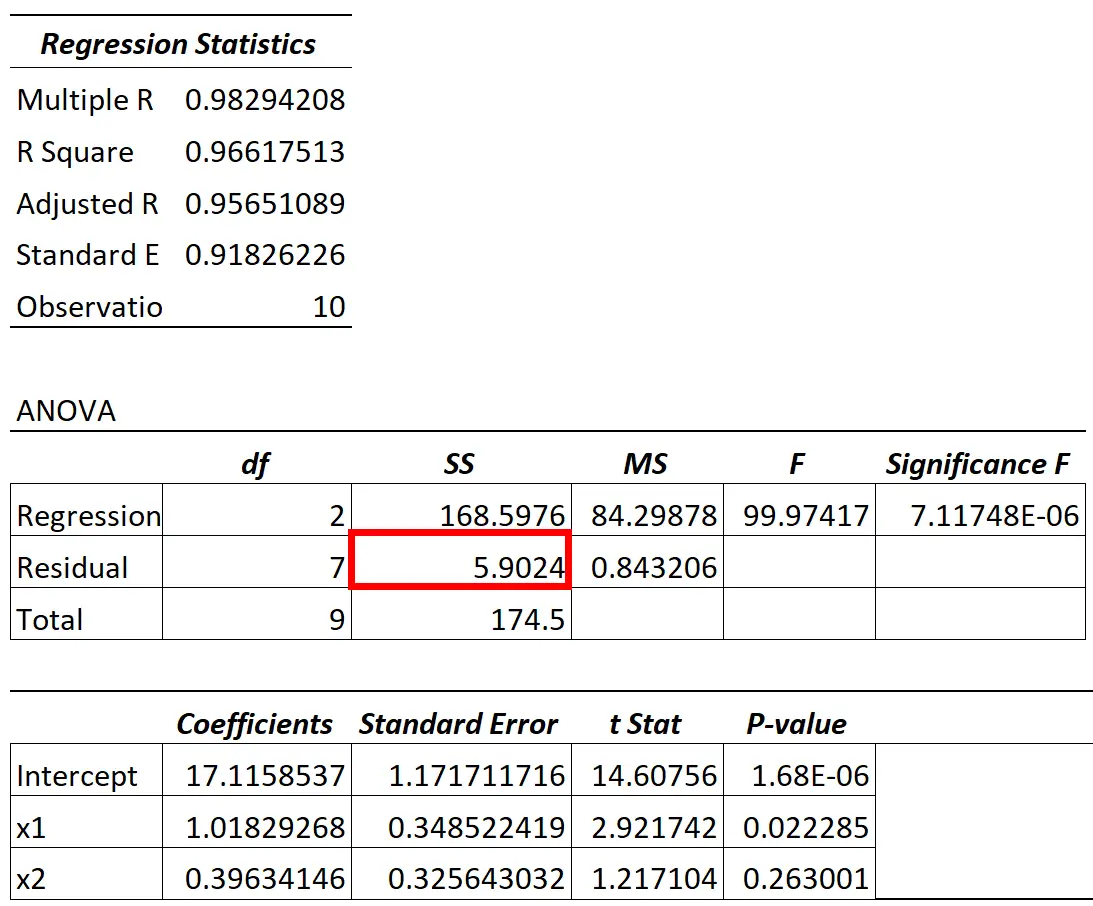
ANOVA 模型的残差方差值可以在残差方差的 SS(“平方和”)列中找到。
模型中残差变异与总变异的比率告诉我们响应变量中无法由模型中的预测变量解释的变异百分比。
例如,在上表中,我们将按如下方式计算该百分比:
- 无法解释的变化 = SS 残差 / SS 总计
- 无法解释的变异 = 5.9024 / 174.5
- 无法解释的变异 = 0.0338
该值也可以使用以下公式计算:
- 无法解释的变异 = 1 – R 2
- 无法解释的变异 = 1 – 0.96617
- 无法解释的变异 = 0.0338
模型的 R 平方值告诉我们可以由预测变量解释的响应变量的变化百分比。
因此,无法解释的变异越低,模型就越有能力使用预测变量来解释响应变量的变异。