如何在sas中计算烹饪距离

库克距离用于识别回归模型中有影响的观测值。

库克距离的公式为：

d _i = (r _i ² / p*MSE) * (h _ii / (1-h _ii ) ² )

金子：

• r _i是第 i^个残基
• p是回归模型中的系数数量
• MSE是均方误差
• h _ii为^{第 i}个杠杆值

本质上，库克距离衡量的是当第 i^个观测值被移除时模型的所有拟合值发生了多少变化。

库克距离的值越大，给定观测的影响力就越大。

一般来说，库克距离大于 4/n（其中n = 总观测值）的任何观测值都被认为具有较大影响。

以下示例显示如何计算 SAS 回归模型中每个观测值的库克距离。

示例：计算 SAS 中厨师的距离

假设我们在 SAS 中有以下数据集：

 /*create dataset*/
data my_data;
    input xy;
    datalines ;
8 41
12 42
12 39
13 37
14 35
16 39
17 45
22 46
24 39
26 49
29 55
30 57
;
run ;

/*view dataset*/
proc print data =my_data;

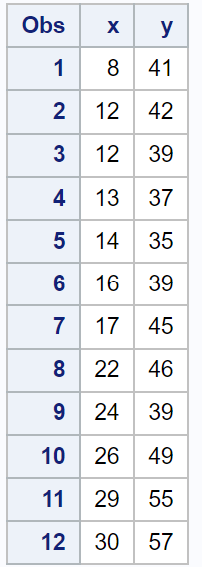
我们可以使用PROC REG对该数据集拟合一个简单的线性回归模型，然后使用OUTPUT语句和COOKD语句来计算回归模型中每个观测值的 Cook 距离：

 /*fit simple linear regression model and calculate Cook's distance for each obs*/
proc reg data =my_data;
    model y=x;
    output out=cooksData cookd =cookd;
run ;

/*print Cook's distance values for each observation*/
proc print data =cooksData;

最终结果表显示原始数据集以及每个观测的 Cook 距离：

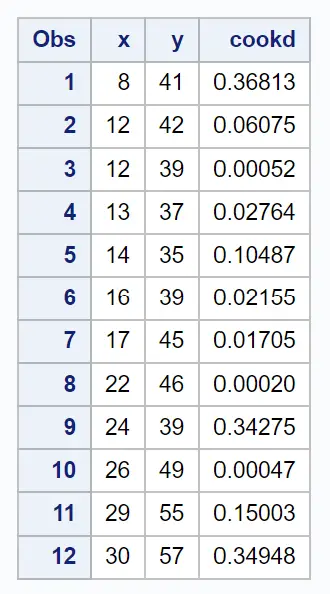
例如，我们可以看到：

• 第一次观测的库克距离为0.36813 。
• 第二次观测的库克距离为0.06075 。
• 第三个观测值的库克距离为0.00052 。

等等。

PROC REG过程还在输出中生成多个诊断图，并且可以在此输出中看到 Cook 距离图：

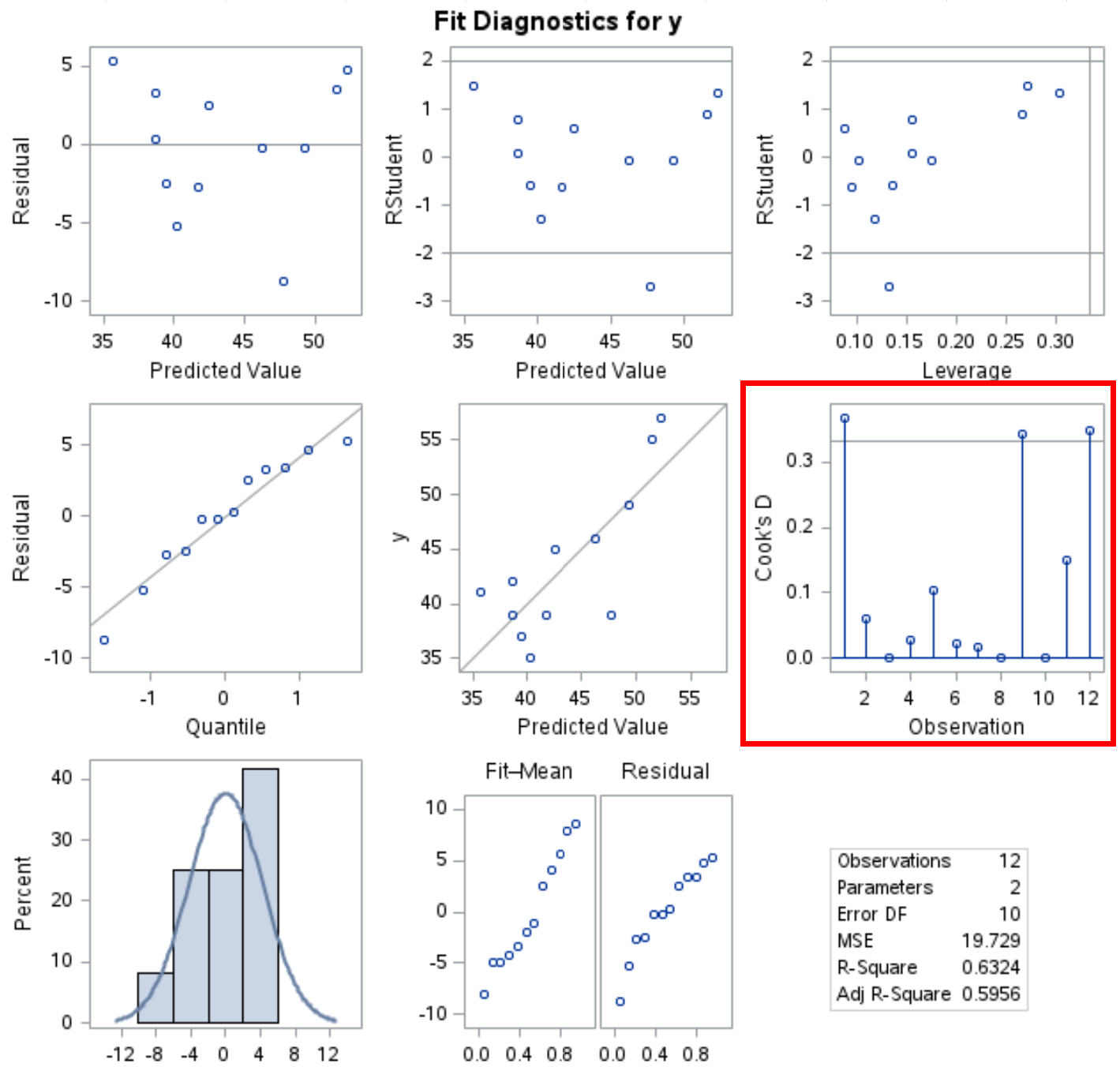
x 轴显示观测数量，y 轴显示每个观测的 Cook 距离。

请注意，截止线位于 4/n（在本例中 n = 12，因此截止值为 0.33），我们可以看到数据集中的三个观测值大于该线。

这表明这些观察结果可能对回归模型有很大影响，也许应该在解释模型结果之前更仔细地检查。

其他资源

以下教程解释了如何在 SAS 中执行其他常见任务：

如何在 SAS 中创建残差图
如何在 SAS 中创建直方图
如何在 SAS 中创建点云
如何识别 SAS 中的异常值