如何在 excel 中执行 fisher 精确检验

Fisher 精确检验用于确定两个 calcategories 变量之间是否存在显着关联。当 2 × 2 表中的一个或多个单元格计数小于 5 时，它通常用作独立性卡方检验的替代方法。

本教程介绍如何在 Excel 中执行 Fisher 精确检验。

示例：Excel 中的 Fisher 精确检验

假设我们想知道性别是否与特定大学对政党的偏好有关。为了探究这一点，我们随机调查了校园内的 25 名学生。按性别划分的民主党或共和党学生人数如下表所示：

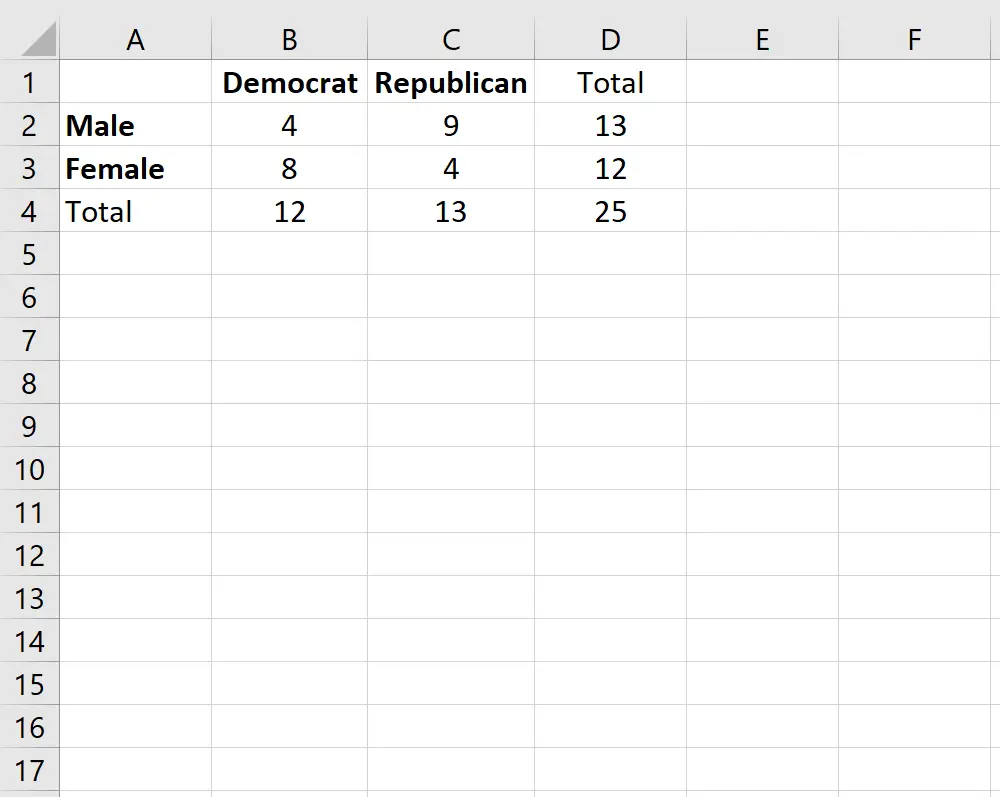
为了确定性别和政党偏好之间是否存在统计上显着的关联，我们可以进行费舍尔精确检验。

虽然Excel没有内置函数来执行此测试，但我们可以使用超几何函数来执行测试，该函数使用以下语法：

=HYPGEOM.DIST(sample_s, number_sample, Population_s, number_pop, 累积)

金子：

• Sample_s = 样本中“成功”的数量
• number_sample = 样本大小
• Population_s = 总体中“成功”的数量
• number_pop = 人口规模
• cumulative = 如果为 TRUE，则返回累积分布函数；如果为 FALSE，则返回概率质量函数。出于我们的目的，我们将始终使用 TRUE。

为了将此函数应用于我们的示例，我们将选择 2×2 表格中的四个单元格之一进行使用。任何单元格都可以，但在此示例中我们将使用值为“4”的左上角单元格。

接下来，我们将为函数填写以下值：

= HYPGEOM.DIST（单个单元格中的值、总列数、总行数、总样本大小、TRUE）

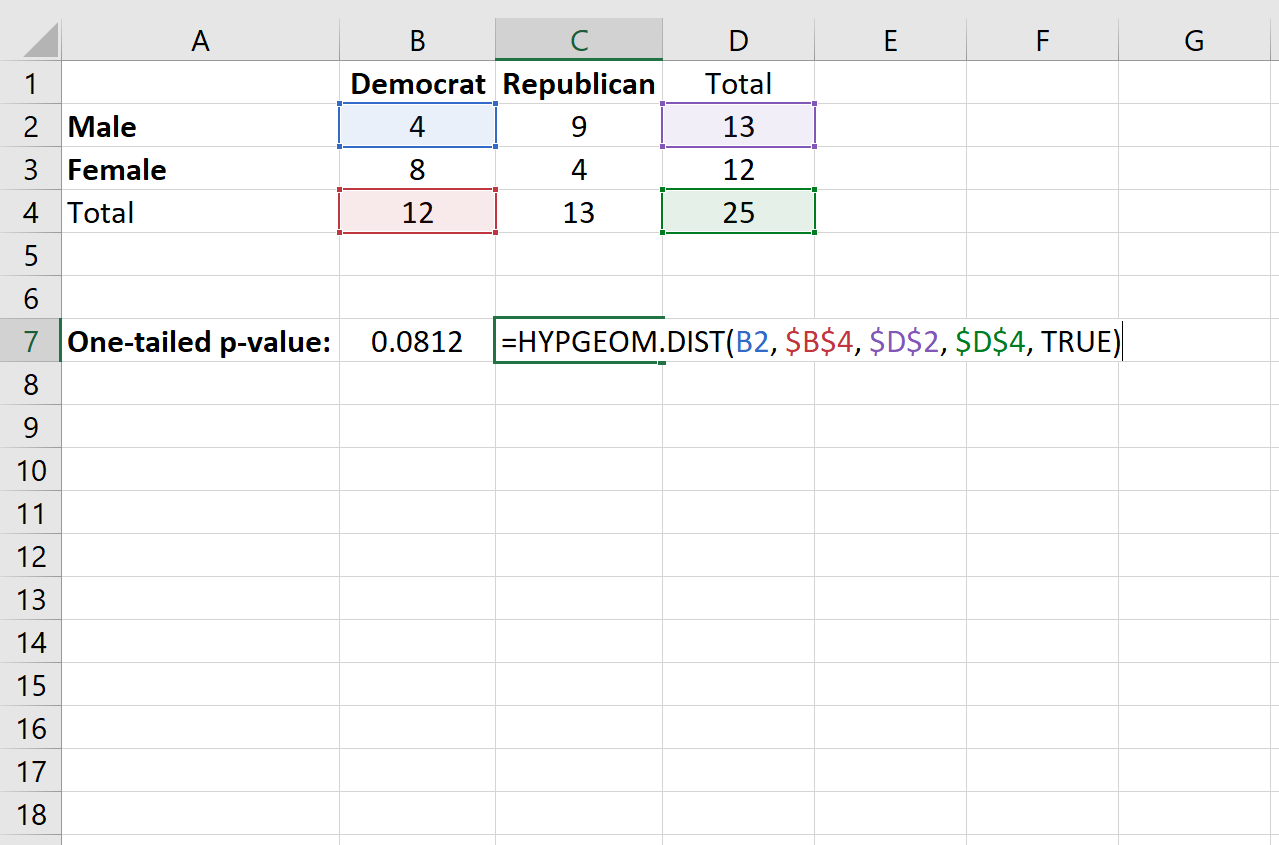
这会产生单边 p 值0.0812 。

为了找到检验的两侧 p 值，我们将添加以下两个概率：

• 在感兴趣的细胞中获得 x“成功”的概率。在我们的例子中，这是获得 4 次成功的概率（我们已经发现该概率为 0.0812）。
• 1 – 在感兴趣的单元格中获得（列总数 – x“成功”）的概率。在本例中，民主党的总列数为 12，因此我们会发现 1 – （8“成功”的概率）

这是我们将使用的公式：

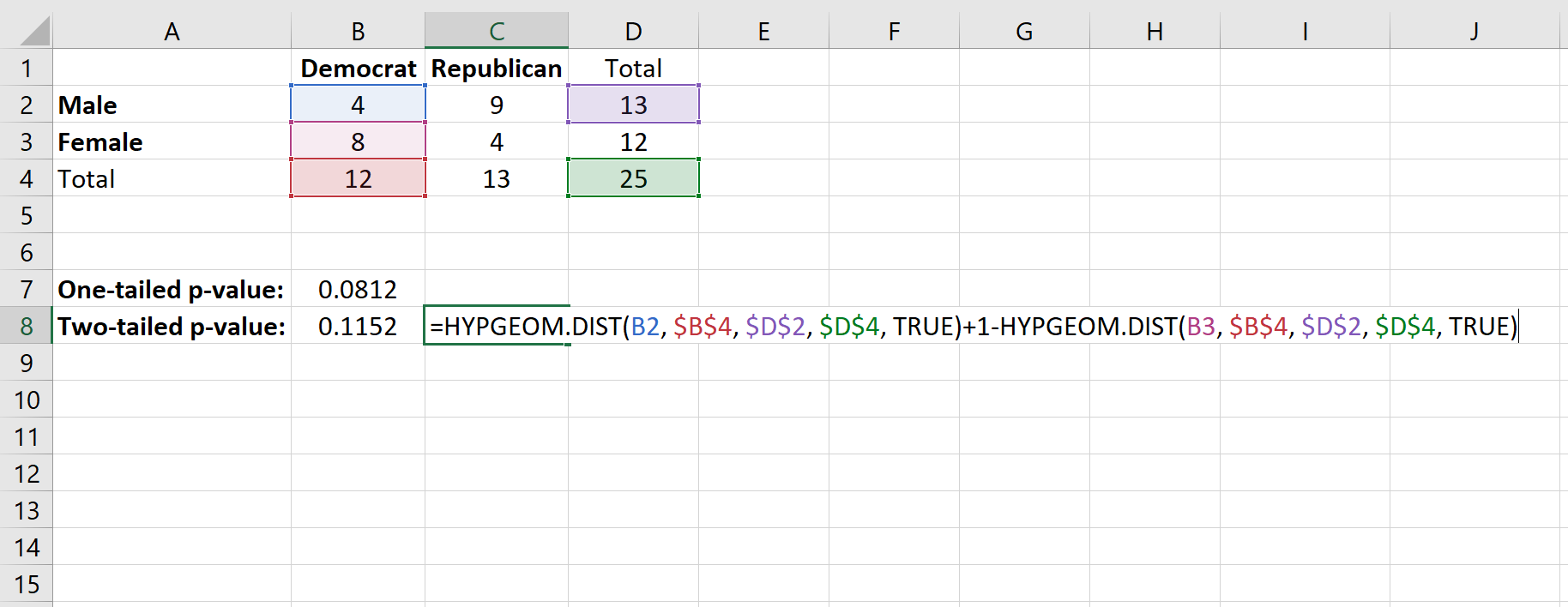
这会产生0.1152的双尾 p 值。

在这两种情况下，无论我们进行单尾检验还是双尾检验，p 值均不小于 0.05，因此我们不能拒绝原假设。换句话说，我们没有足够的证据表明性别和政党偏好之间存在显着关联。

其他资源

如何在 Excel 中执行卡方独立性检验
如何在 Excel 中执行卡方拟合检验
如何在 Excel 中计算 Cramer 的 V