瑞利分布简介
瑞利分布是一种连续概率分布,用于对只能取等于或大于零的值的随机变量进行建模。
其概率密度函数如下:
f(x; σ) = (x/σ 2 )e -x 2 /(2σ 2 )
其中 σ 是分布的尺度参数。
瑞利分布的性质
瑞利分布具有以下性质:
- 平均值: σ√π /2
- 偏差: ((4-π)/2)σ 2
- 众数: σ
由于 π 具有已知的数值,我们可以将属性简化如下:
- 平均值: 1.253σ
- 偏差: 0.429σ 2
- 众数: σ
瑞利分布的可视化
下图显示了瑞利分布的形状,因为它采用不同的尺度参数值:
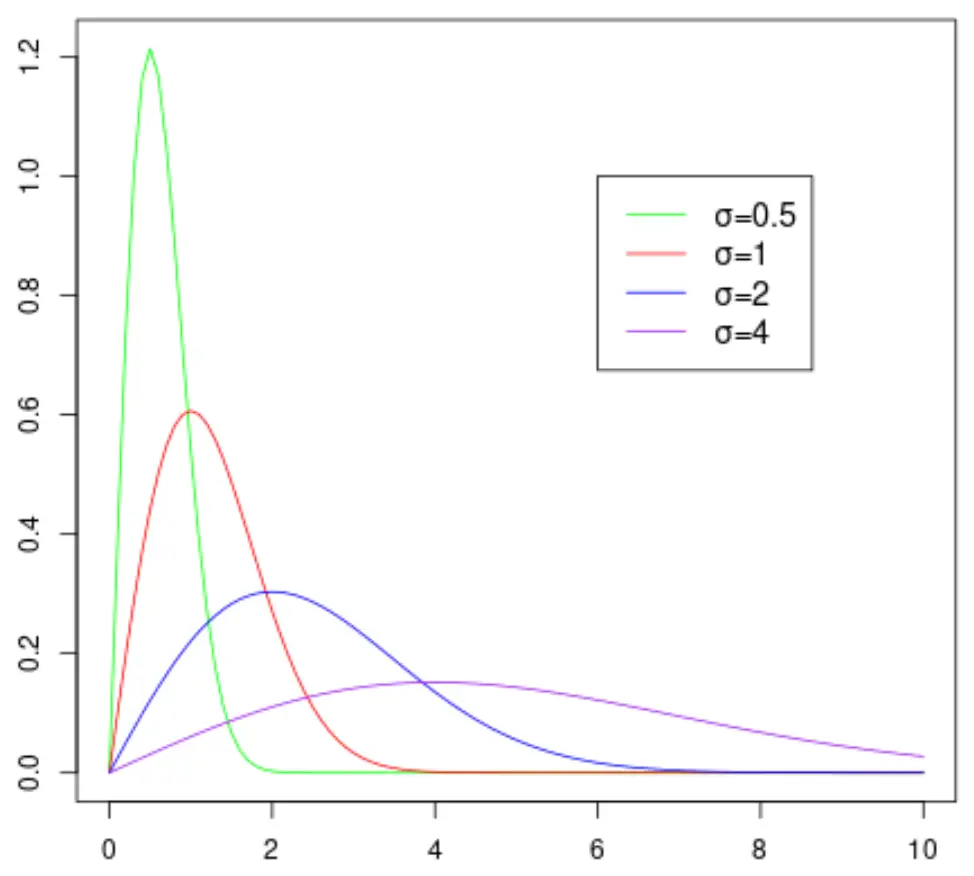
请注意,尺度参数 σ 的值越大,分布就越宽。
奖励:对于那些好奇的人,我们使用以下 R 代码来生成上面的图表:
#load VGAM package library (VGAM) #create density plots curve(drayleigh(x, scale = 0.5), from=0, to=10, col='green') curve(drayleigh(x, scale = 1), from=0, to=10, col='red', add=TRUE) curve(drayleigh(x, scale = 2), from=0, to=10, col='blue', add=TRUE) curve(drayleigh(x, scale = 4), from=0, to=10, col='purple', add=TRUE) #add legend legend(6, 1, legend=c("σ=0.5", "σ=1", "σ=2", "σ=4"), col=c("green", "red", "blue", "purple"), lty=1, cex=1.2)
与其他发行版的关系
瑞利分布与其他概率分布有以下关系:
1.当尺度参数(σ)等于1时,瑞利分布等于2个自由度的卡方分布。
2.瑞利分布是形状参数 k = 2 的威布尔分布的特例。
3.尺度参数为 σ 的瑞利分布等于 Rice(0, σ) 的莱斯分布。
应用领域
在实践中,瑞利分布用于各种应用,包括:
1.瑞利分布用于模拟海洋中波浪的行为,包括波浪到达波峰所需的时间以及波浪达到的最大高度。
2.瑞利分布用于对磁共振成像(通常称为 MRI)中背景数据的行为进行建模。
3.瑞利分布用于营养领域,用于模拟人类和动物的营养水平与营养反应之间的关系。
其他资源
以下教程提供了有关统计中其他分布的更多信息: