百分位数（统计）

本文解释了什么是百分位数以及如何计算它。您将找到已解决的百分位数练习，此外，您将能够使用在线计算器计算数据样本的任何百分位数。

什么是百分位数？

在统计学中，百分位数是将一组有序数据分为一百等份的值。因此，百分位表示数据集的百分比低于该值的值。

例如，第 35 个百分位值高于观测数据的 35%，但低于其余数据。

百分位数由大写字母P和百分位数索引表示，即第1个百分位数为P ₁ ，第40个百分位数为P ₄₀ ，第79个百分位数为P ₇₉ ，依此类推。

👉您可以使用下面的计算器来计算任何数据集的百分位数。

同样，百分位数与四分位数、五分位数和十分位数一起衡量非中心位置。您可以在我们的网站上查看每种分位数类型的含义。

应该注意的是，百分位数一词也用于将婴儿的体重和身高与其他婴儿的标准值进行比较，因为有记录值的生长表可以帮助确定婴儿的生长是否正确。 。 。

如何计算百分位数

要计算统计数据系列中百分位数的位置，必须将百分位数乘以数据点总数加一的总和，然后将结果除以一百。

因此，百分位公式为：

请注意：这个公式告诉我们百分位数的位置，但不是它的值。百分位将是位于由公式获得的位置的数据。

然而，有时这个公式的结果会给我们一个十进制数，因此我们必须根据结果是否是十进制数来区分两种情况：

• 如果公式的结果是不带小数部分的数字，则百分位数对应于上式所提供位置的数据。
• 如果公式结果是带小数部分的数字，则使用以下公式计算精确的百分位数：

其中x _i和x _i+1为第一个公式得到的数所在位置的数字， d为第一个公式得到的数的小数部分。

您现在可能认为查找统计样本或总体的百分位数很复杂，因为该方法涉及许多步骤，但实际上很简单。阅读以下两个具体示例，相信您会更好地理解。

注意：科学界尚未就如何计算百分位数达成完全一致，因此您可以找到一本统计书籍，其解释略有不同。

百分位数计算示例

正如您在上面关于如何查找样本百分位数的说明中看到的，计算结果会根据第一个公式的结果是否为小数而有所不同。这就是为什么您会在下面找到两个已解决的示例，每种情况一个。

实施例1

• 根据下表中显示的数据，计算第 1、43 和 89 个百分位数。

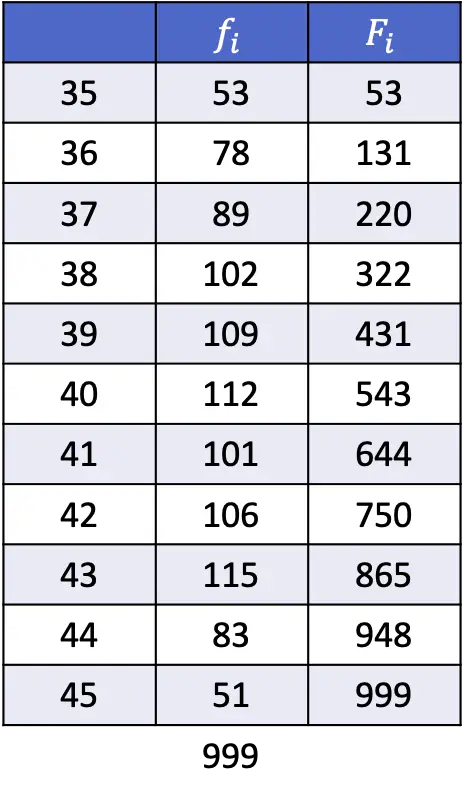
如上一节所述，查找百分位位置的公式为：

在本例中，本练习的样本量为 999 个统计数据，因此要计算第一个百分位数的位置，我们需要将n替换为 999，将k替换为 1：

因此，第一个百分位数将是累积绝对频率立即大于 10 的百分位数，在本例中为 35，因为它的累积绝对频率为 53。

要确定第 43 个百分位数，您必须使用相同的公式，但显然，这次我们将k替换为 43。

紧邻 430 之上的绝对累积频率是数据 39 的 431，因此第 43 个百分位数等于 39。

最后，我们应用相同的公式来获得第 89 个百分位数：

值 44 的累积绝对频率是 948，它立即大于 890。因此，第 89 个百分位数是 44。

实施例2

• 查找以下数据系列的第 35 个和 67 个百分位数：

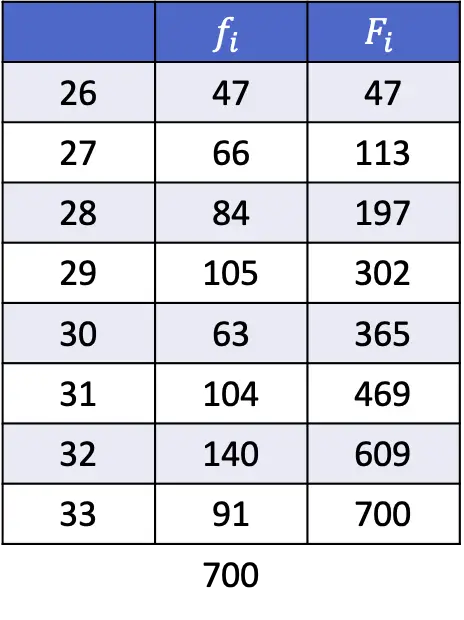
即使在本练习中我们需要进行更多计算，原理仍然是相同的：我们必须使用以下表达式计算百分位位置。

因此，为了计算第 35 个百分位，我们将k替换为 35，将n替换为数据总数，即 700：

但是这次我们从公式中得到了一个小数，因此我们需要应用以下代数表达式来计算精确的百分位值：

第一个公式给出的数字是245.35，因此第35个百分位数位于位置245和246之间，分别对应于值29和29。因此， x _i为29， x _i+1为29， d为所得数的小数部分，即0.35。

要找到第 67 个百分位，我们需要使用相同的方法。我们首先计算百分位位置：

得到的数字 469.67 表明百分位数将位于位置 469 和 470 之间，其值为 31 和 32。因此，我们在过程中使用第二个公式来查找准确的百分位数值：

百分位数计算器

在以下计算器中输入统计数据集和要计算的百分位数。数据必须用空格分隔，并使用句点作为小数点分隔符输入。

• 百分位数 =

分组数据中的百分位数

要计算数据分组时的百分位数，我们首先需要使用以下公式找到百分位数所属的组或类：

因此，百分位数将位于其绝对频率立即大于先前表达式中获得的数字的区间内。

一旦我们知道了百分位数所属的区间，我们就必须应用以下公式来找到百分位数的准确值：

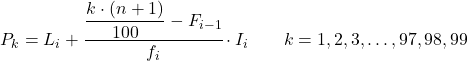
金子：

• _Li是百分位数所在区间的下限。
• n是观测值总数。
• F _i-1是前一个间隔的累积绝对频率。
• f _i是百分位数所在区间的绝对频率。
• I _i是百分位数间隔的宽度。

下面是有关如何在数据以区间表示时获取百分位数的分步练习。具体来说，计算第 29、52 和 98 个百分位数。

该样本中的数据按区间分组，因此我们需要执行两个步骤来确定百分位数：首先我们需要找到百分位数所属的区间，然后应用公式计算百分位数的精确值。百分位数。

因此，我们使用以下表达式找到第 29 个百分位的位置：

百分位数区间将是累积绝对频率立即大于 145.29 的区间，在本例中是累积绝对频率为 175 的区间 [350.375)。一旦我们知道了百分位数区间，我们就可以应用以下公式来计算它准确值：

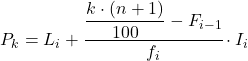
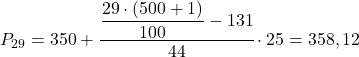
现在我们重复相同的过程来计算第 52 个百分位数。我们首先计算它的区间：

第 52 个百分位间隔为 [400.425)，因为其累积绝对频率 (298) 紧邻 260.52 以上。因此，百分位的确切值将是：

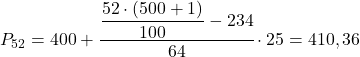
最后，我们将找到第 98 个百分位。与往常一样，我们首先计算它所在的区间：

一旦我们知道了百分位数所在的区间，我们就可以使用以下公式计算其精确值：