什么是皮尔逊残差? (定义&;示例)
皮尔逊残差用于独立性卡方检验中,以分析列联表中观察到的细胞数与预期细胞数之间的差异。
皮尔逊残差的计算公式为:
r ij = (O ij – E ij ) / √ E ij
金子:
- r ij :第i列第 j行单元格的皮尔逊残差
- O ij :第i列第 j行单元格的观测值
- E ij :第i列第 j行单元格的期望值
类似的衡量标准是标准化(调整后)皮尔逊残差,其计算如下:
r ij = (O ij – E ij ) / √ E ij (1-n i+ )(1-n +j )
金子:
- r ij :第i列第 j行单元格的皮尔逊残差
- O ij :第i列第 j行单元格的观测值
- E ij :第i列第 j行单元格的期望值
- p i+ :行总计除以总计
- p + j :列总计除以总计
标准化 Pearson 残差呈正态分布,平均值为 0,标准差为 1。任何绝对值高于特定阈值(例如 2 或 3)的标准化 Pearson 残差均表示缺乏拟合。
以下示例展示了如何在实践中计算 Pearson 残差。
示例:Pearson 残差的计算
假设研究人员想要使用卡方独立性检验来确定性别是否与对政党的偏好相关。
他们决定对 500 名选民进行简单随机抽样,并询问他们的政党偏好。
以下列联表显示了调查结果:
| 共和党人 | 民主党人 | 独立的 | 全部的 | |
| 男性 | 120 | 90 | 40 | 250 |
| 女性 | 110 | 95 | 45 | 250 |
| 全部的 | 230 | 185 | 85 | 500 |
在计算 Pearson 残差之前,我们必须首先计算列联表中每个单元格的预期计数。为此,我们可以使用以下公式:
期望值=(行数总和*列数总和)/表总和。
例如,共和党男性的期望值为: (230*250) / 500 = 115 。
我们可以重复此公式来获取每个表格单元格的期望值:
| 共和党人 | 民主党人 | 独立的 | 全部的 | |
| 男性 | 115 | 92.5 | 42.5 | 250 |
| 女性 | 115 | 92.5 | 42.5 | 250 |
| 全部的 | 230 | 185 | 85 | 500 |
然后我们可以计算表中每个单元格的皮尔逊残差。
例如,包含共和党男性的单元格的皮尔逊残差计算如下:
- r ij = (O ij – E ij ) / √ E ij
- rij = (120 – 115) / √ 115
- rij = 0.466
我们可以重复此公式来获取表中每个单元格的皮尔逊残差:
| 共和党人 | 民主党人 | 独立的 | |
| 男性 | 0.446 | -0.259 | -0.383 |
| 女性 | -0.446 | 0.259 | 0.383 |
然后我们可以计算表中每个单元格的标准化皮尔逊残差。
例如,包含共和党男性的单元格的标准化皮尔逊残差计算如下:
- r ij = (O ij – E ij ) / √ E ij (1-p i+ )(1-p +j )
- rij = (120 – 115) / √ 115(1-250/500)(1-230/500)
- rij = 0.897
我们可以重复此公式以获得表中每个单元格的标准化皮尔逊残差:
| 共和党人 | 民主党人 | 独立的 | |
| 男性 | 0.897 | -0.463 | -0.595 |
| 女性 | -0.897 | 0.463 | 0.595 |
我们可以看到,没有一个标准化 Pearson 残差的绝对值大于 3,这表明没有一个单元格会导致显着缺乏拟合。
如果我们使用 这个在线计算器执行独立性卡方检验,我们会发现检验的 p 值为0.649198 。
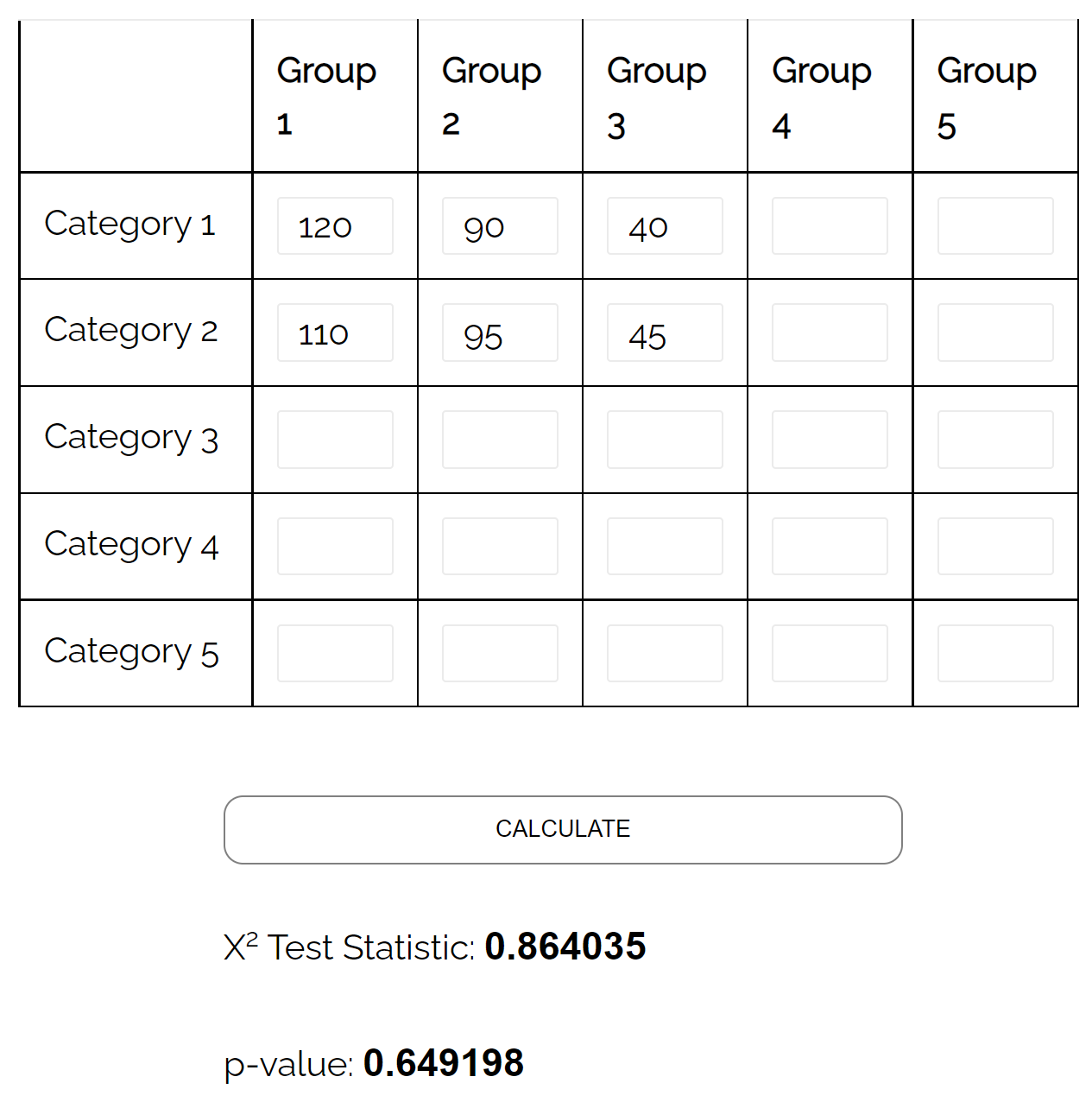
由于该 p 值不小于 0.05,因此我们没有足够的证据表明性别与政党偏好之间存在关联。
其他资源
以下教程说明如何使用不同的统计软件执行卡方独立性检验: