皮尔逊相关系数

Pearson 相关系数（也称为“乘积矩相关系数”）是两个变量X和Y之间线性关联的度量。它的值介于 -1 和 1 之间，其中：

• -1 表示两个变量之间完全负线性相关
• 0 表示两个变量之间不存在线性相关
• 1 表示两个变量之间存在完全正线性相关

求皮尔逊相关系数的公式

用于查找数据样本的皮尔逊相关系数（表示为r ）的公式为（ 来自维基百科）：

您可能永远不需要手动计算这个公式，因为您可以使用软件来计算这个公式，但是通过示例来了解这个公式的确切作用是有帮助的。

假设我们有以下数据集：

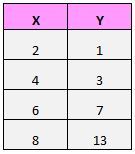
如果我们将这些对 (X, Y) 绘制在散点图上，它将如下所示：

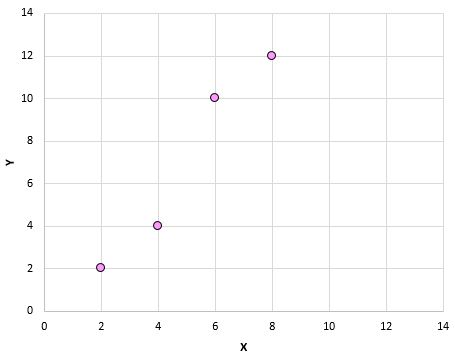
只需查看该散点图，我们就可以看到变量 X 和 Y 之间存在正相关关系：随着 X 的增加，Y 也趋于增加。但为了准确量化这两个变量的正相关程度，我们需要找到皮尔逊相关系数。

我们只关注公式的分子：

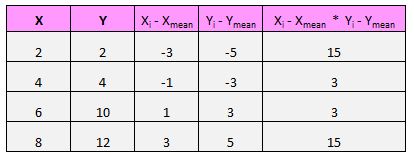
对于数据集中的每一对 (X, Y)，我们需要找到 x 值与平均 x 值之间的差值、y 值与平均 y 值之间的差值，然后将这两个数字相乘。

例如，我们的第一对 (X, Y) 是 (2, 2)。该数据集中 x 的平均值为 5，该数据集中 y 的平均值为 7。因此该对的 x 值与 x 的平均值之差为 2 – 5 = -3。该对的 y 值与平均 y 值之差为 2 – 7 = -5。然后，当我们将这两个数字相乘时，我们得到 -3 * -5 = 15。

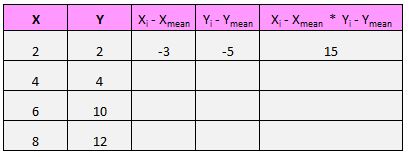
这是我们刚刚所做的直观概述：

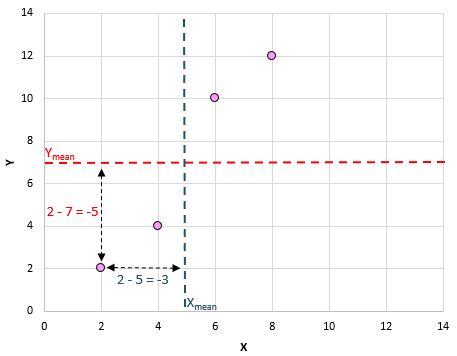
然后对每一对执行以下操作：

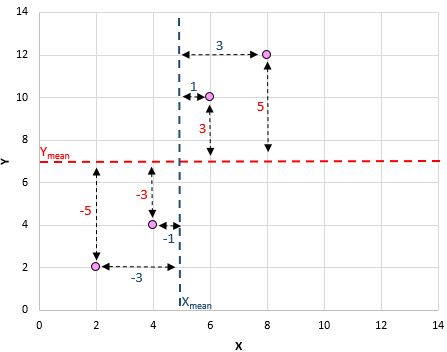
获取公式分子的最后一步是将所有这些值简单地添加在一起：

15 + 3 +3 + 15 = 36

然后公式的分母告诉我们找到 x 和 y 的所有平方差之和，然后将这两个数字相乘，然后取平方根：

首先我们要求 x 和 y 之差的平方和：

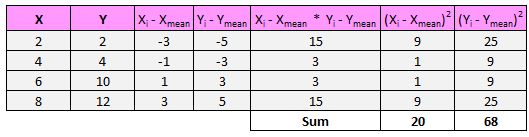
接下来，我们将这两个数字相乘：20 * 68 = 1,360。

最后，我们求平方根：√ 1,360 = 36.88

所以我们发现公式的分子是36，分母是36.88。这意味着我们的皮尔逊相关系数为 r = 36 / 36.88 = 0.976

这个数字接近 1，表明我们的变量X和Y之间存在很强的正线性关系。这证实了我们在散点图中观察到的关系。

查看相关性

请记住，皮尔逊相关系数告诉我们两个变量之间的线性关系类型（正、负、无）以及这种关系的强度（弱、中等、强）。

当我们创建两个变量的散点图时，我们可以看到两个变量之间的真实关系。以下是我们可能观察到的多种类型的线性关系：

强正相关关系：随着 x 轴上的变量增加，y 轴上的变量也会增加。这些点紧密聚集，表明存在很强的关系。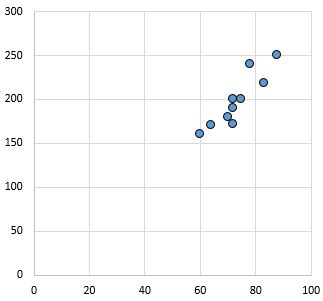

皮尔逊相关系数： 0.94

弱正关系：随着 x 轴上的变量增加，y 轴上的变量也会增加。这些点相当分散，表明关系较弱。

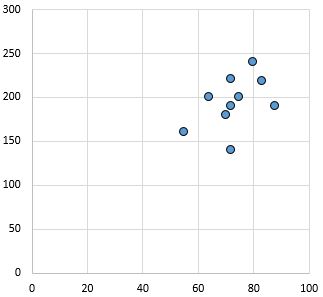
皮尔逊相关系数： 0.44

无关系：变量之间没有明确的关系（正或负）。

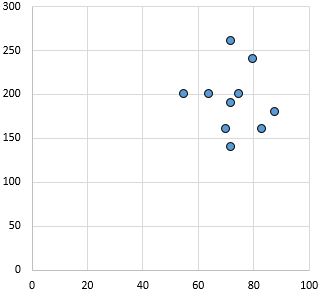
皮尔逊相关系数： 0.03

强负关系：随着 x 轴上的变量增加，y 轴上的变量减少。这些点紧密地堆积在一起，表明存在很强的关系。

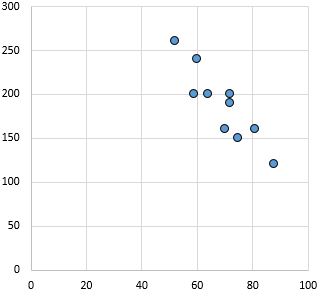
皮尔逊相关系数： -0.87

弱负关系：随着 x 轴上的变量增加，y 轴上的变量减少。这些点相当分散，表明关系较弱。

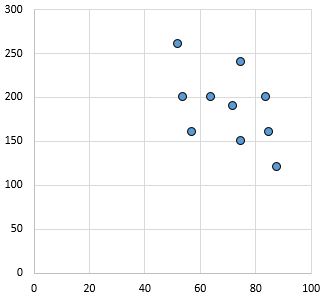
皮尔逊相关系数： – 0.46

测试 Pearson 相关系数的显着性

当我们找到一组数据的皮尔逊相关系数时，我们通常会使用来自较大总体的数据样本。这意味着即使两个变量在总体中实际上不相关，也可以找到两个变量的非零相关性。

例如，假设我们为整个总体中每个数据点的变量X和Y创建一个散点图，如下所示：

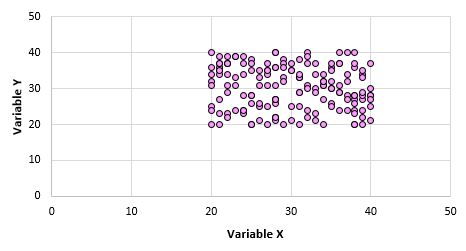
很明显，这两个变量不相关。然而，当我们从总体中抽取 10 个点的样本时，我们可能会选择以下点：

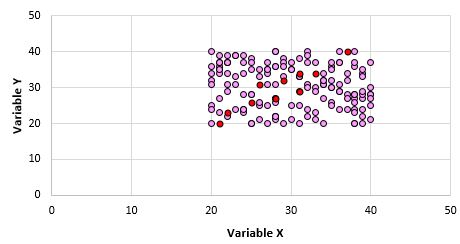
我们可以看到，该点样本的 Pearson 相关系数为 0.93，表明尽管总体相关性为零，但仍存在很强的正相关性。

为了检验两个变量之间的相关性是否具有统计显着性，我们可以找到以下检验统计量：

检验统计量 T = r * √ (n-2) / (1-r ² )

其中n是样本中的对数， r是 Pearson 相关系数，T 检验统计量遵循 n-2 自由度的分布。

让我们回顾一下如何测试 Pearson 相关系数的显着性的示例。

例子

以下数据集显示了 12 个人的身高和体重：

下面的散点图显示了这两个变量的值：

这两个变量的 Pearson 相关系数为 r = 0.836。

检验统计量 T = 0.836 * √ (12 -2) / (1-0.836 ² ) = 4.804。

根据我们的t 分布计算器，自由度为 10 的分数 4.804 的 p 值为 0.0007。由于 0.0007 < 0.05，我们可以得出结论，本例中体重和身高之间的相关性在 alpha = 0.05 时具有统计显着性。

防范措施

尽管皮尔逊相关系数可用于告诉我们两个变量是否具有线性关联，但在解释皮尔逊相关系数时，我们需要记住三件事：

1.相关性并不意味着因果关系。并不是因为两个变量相关，其中一个变量必然会导致另一个变量出现的频率增加或减少。一个典型的例子是冰淇淋销售与鲨鱼袭击之间的正相关关系。当冰淇淋销量在一年中的某些时候增加时，鲨鱼袭击事件也往往会增加。

这是否意味着吃冰淇淋会导致鲨鱼袭击？当然不是！这仅仅意味着在夏天，冰的消耗和鲨鱼袭击往往会增加，因为冰在夏天更受欢迎，更多的人在夏天进入海洋。

2. 相关性对异常值很敏感。极端异常值可以显着改变皮尔逊相关系数。考虑下面的例子：

变量X和Y的 Pearson 相关系数为0.00 。但想象一下数据集中有一个异常值：

然而，这两个变量的 Pearson 相关系数为0.878 。这个异常值改变了一切。这就是为什么在计算两个变量的相关性时，最好使用散点图可视化变量来检查异常值。

3. Pearson 相关系数不能捕捉两个变量之间的非线性关系。假设我们有两个具有以下关系的变量：

这两个变量的 Pearson 相关系数为 0.00，因为它们不具有线性关系。然而，这两个变量具有非线性关系：y 值只是 x 值的平方。

使用皮尔逊相关系数时，请记住您只是测试两个变量是否线性相关。即使皮尔逊相关系数告诉我们两个变量不相关，它们仍然可能具有某种类型的非线性关系。这是在分析两个变量之间的关系时创建散点图很有用的另一个原因：它可以帮助您检测非线性关系。