如何在 sas 中执行 box-cox 转换
Box-Cox 变换是将非正态分布的数据集变换为更正态分布的数据集的常用方法。
此方法背后的基本思想是使用以下公式找到 λ 值,使变换后的数据尽可能接近正态分布:
- y(λ) = (y λ – 1) / λ 如果 y ≠ 0
- y(λ) = log(y) 如果 y = 0
我们可以使用PROC TRANSREG过程确定 SAS 中 λ 的最佳值。
以下示例展示了如何在实践中使用此过程。
示例:SAS 中的 Box-Cox 变换
假设我们在 SAS 中有以下数据集:
/*create dataset*/ data my_data; input xy; datalines ; 7 1 7 1 8 1 3 2 2 2 4 2 4 2 6 2 6 2 7 3 5 3 3 3 3 6 5 7 8 8 ; run; /*view dataset*/ proc print data =my_data;
假设我们使用PROC REG对该数据集拟合一个简单的线性回归模型,使用x作为预测变量, y作为响应变量。
/*fit simple linear regression model*/ proc reg data =my_data; model y = x; run ;
在输出诊断图中,我们可以显示残差与分位数图(中间行最左边的图),以查看残差在模型中是否近似正态分布:
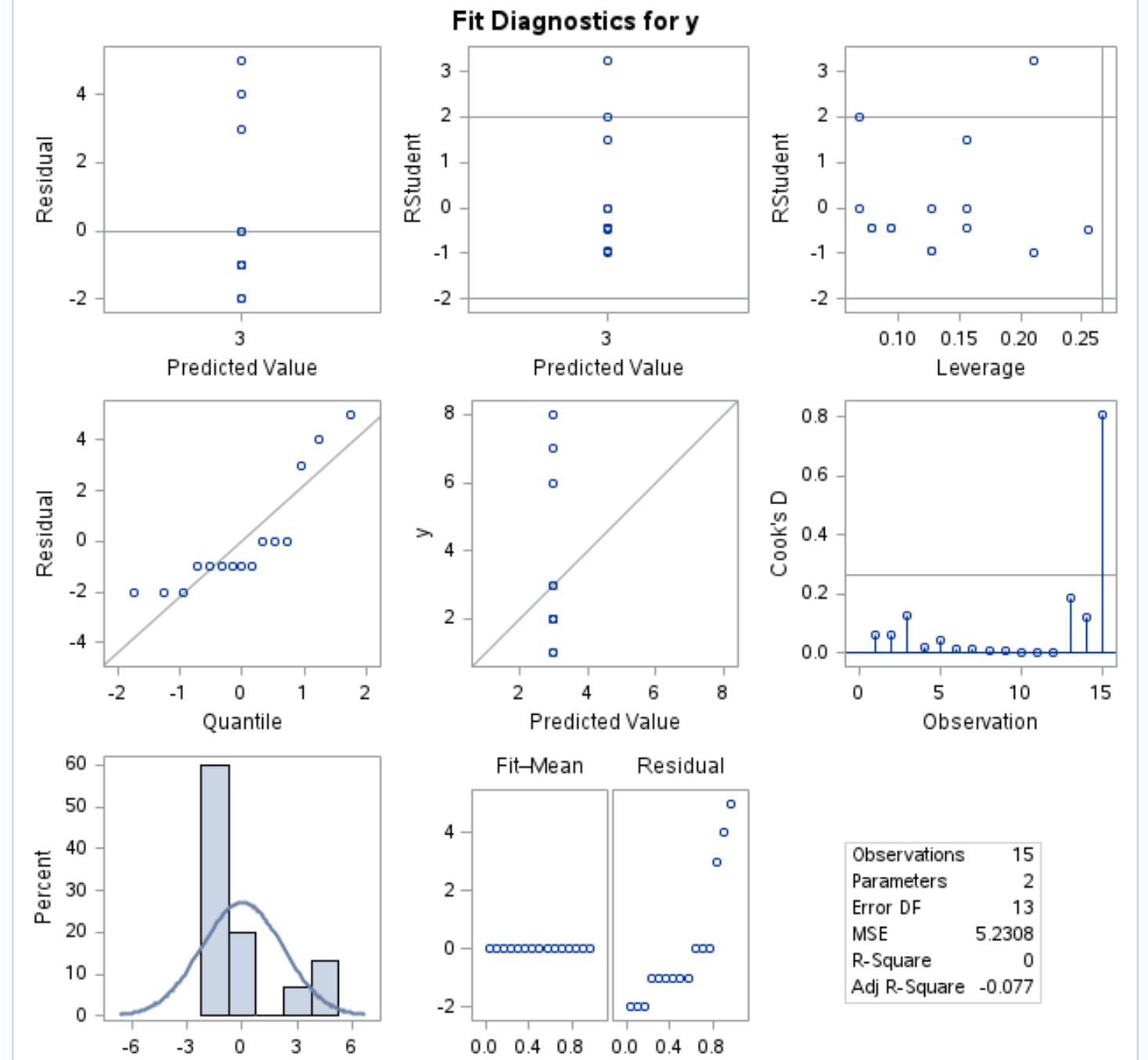
如果残差大约沿着图的右对角线分布,我们通常假设残差呈正态分布。
从图中我们可以看到残差不太遵循直线对角线。
这表明回归模型中的响应变量可能不呈正态分布。
由于响应变量不是正态分布的,我们可以使用PROC TRANSREG来识别 λ 的值,我们可以用它来转换响应变量,使其更服从正态分布:
/*perform box-cox transformation*/ proc transreg data =my_data; model boxcox (y) = identity (x); run ;
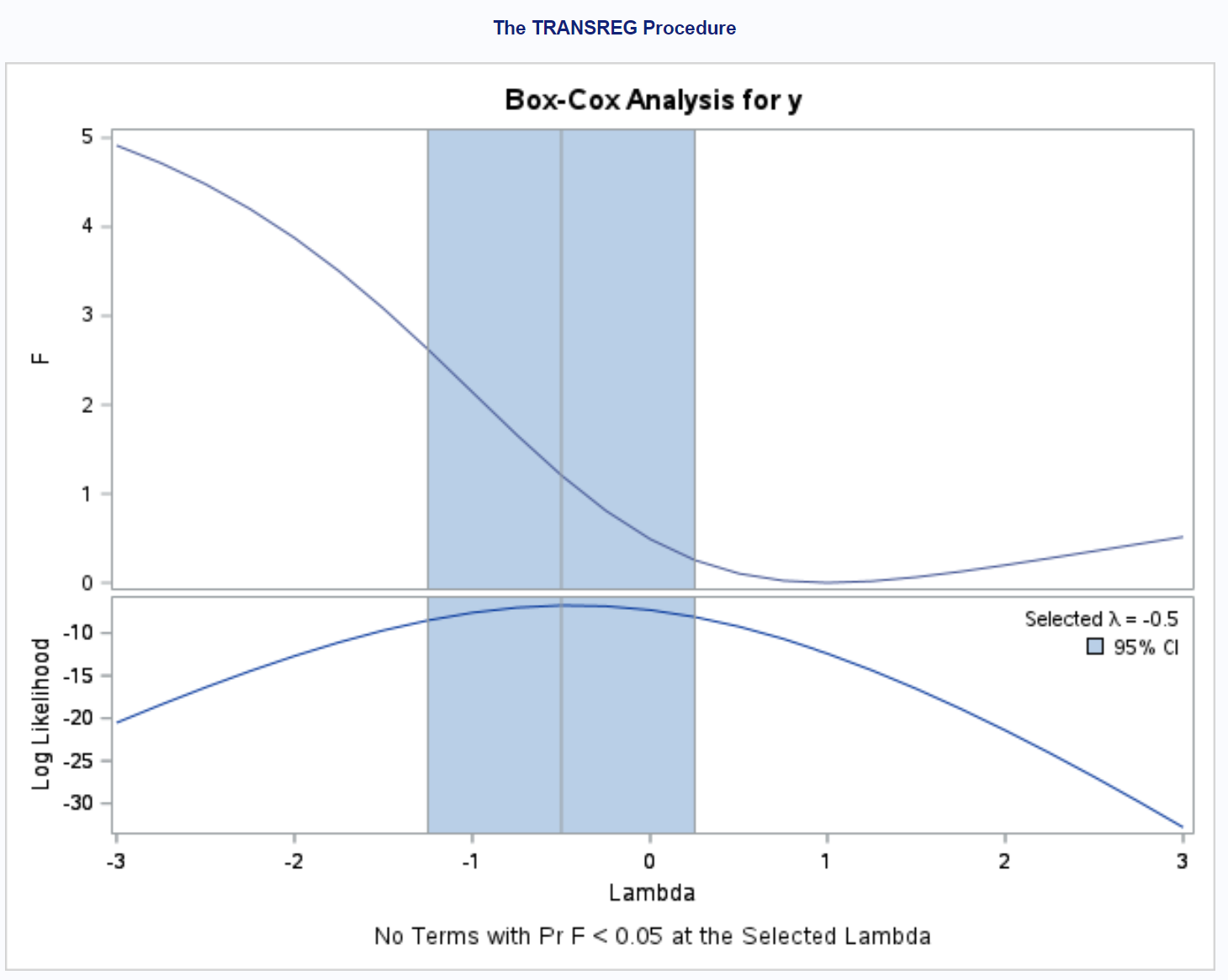
输出告诉我们选择的 λ 值是 – 0.5 。
因此,我们可以通过用变量y = (y -0.5 – 1) / -0.5替换原始响应变量y来拟合简单的线性回归模型。
以下代码展示了如何执行此操作:
/*create new dataset that uses box-cox transformation to create new y*/
data new_data;
set my_data;
new_y = (y**(-0.5) - 1) / -0.5;
run ;
/*fit simple linear regression model using new response variable*/
proc reg data =new_data;
model new_y = x;
run ;
在残差与残差中该模型输出的分位数图,我们可以看到残差沿着直线对角线更加接近:
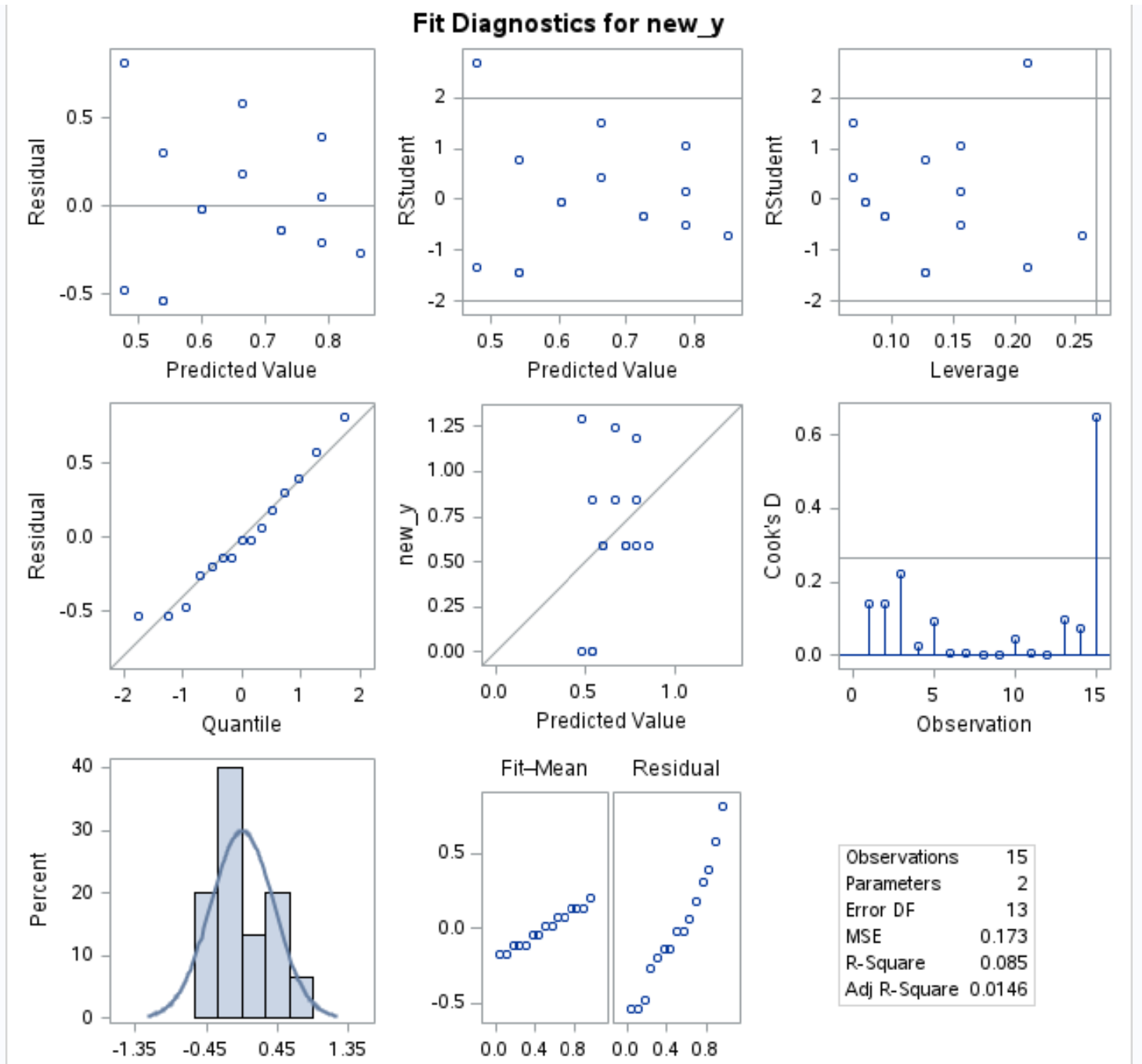
这表明 box-cox 变换模型的残差更加正态分布,满足 线性回归的主要假设之一。
其他资源
以下教程解释了如何在 SAS 中执行其他常见任务:
如何在 SAS 中使用 Proc Univariate 进行正态性检验
如何在 SAS 中创建残差图
如何在 SAS 中执行 Levene 检验