离散均匀分布

本文解释了什么是离散均匀分布及其特征公式是什么。同样，您将能够看到离散均匀分布的图形表示及其属性。

什么是离散均匀分布？

离散均匀分布是一种离散概率分布，其中所有值都是等概率的，即在离散均匀分布中，所有值出现的概率相同。

例如，骰子的滚动可以用离散均匀分布来定义，因为所有可能的结果（1、2、3、4、5 或 6）具有相同的发生概率。

一般来说，离散均匀分布有两个特征参数a和b ，它们定义了分布可以取的可能值的范围。因此，当变量由离散均匀分布定义时，它被写为Uniform(a,b) 。

离散均匀分布可以用来描述随机实验，因为如果所有结果具有相同的概率，则意味着实验是随机的。

离散均匀分布公式

现在我们知道了离散均匀分布的定义，我们将看到允许我们计算这种类型分布的值出现概率的公式是什么。

离散均匀分布的概率函数是常数，其值等于可能结果总数的一。因此，离散均匀分布的公式如下：

另一方面，离散均匀分布的累积概率函数的公式如下：

金子

和

是离散均匀分布的特征参数。

离散均匀分布图

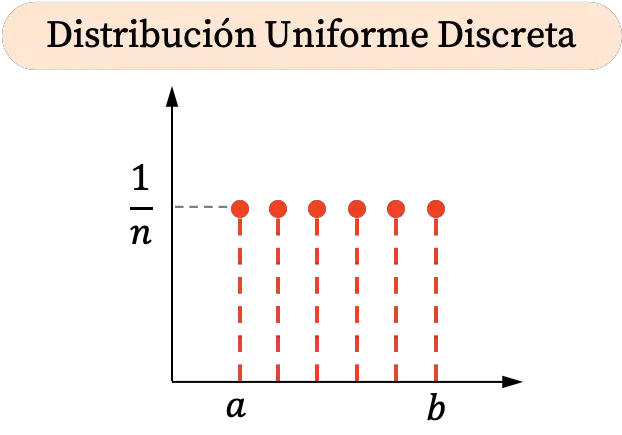
由于离散均匀分布只能在一个区间内取某些值，因此它的图形表示由点组成。此外，所有概率都相等，因此离散均匀分布中的所有点都具有相同的垂直坐标。

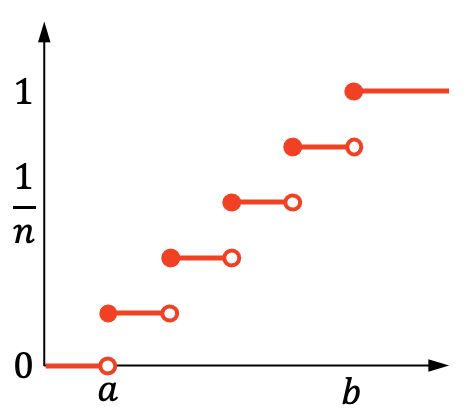
另一方面，离散均匀分布的累积概率图如下：

离散均匀分布的特征

离散均匀分布具有以下特点：

• 离散均匀分布由两个整数参数a和b定义，它们确定分布的可能值的范围。

• 离散均匀分布的均值等于其两个特征参数之和除以二。

• 离散均匀分布的中位数等于其均值，因此可以使用相同的表达式进行计算：

• 离散均匀分布的方差等于结果总数的平方减一除以十二。

• 离散均匀分布关于其均值对称，因此，该概率分布的偏度系数为零。

• 离散均匀分布的峰度可以使用以下表达式计算：

离散均匀分布和连续均匀分布

最后，我们将了解离散均匀分布和连续均匀分布之间的区别，因为它们是两种相似的概率分布类型，但存在很大差异。

离散均匀分布和连续均匀分布之间的区别在于它们可能的值。离散均匀分布只能取某个区间内的某些值，而连续均匀分布可以取其定义的区间内的任意值。

一般来说，离散均匀分布只能取整数值，而连续均匀分布也可以取小数值。