简单线性回归

本文解释了统计学中的简单线性回归是什么以及它是如何执行的。同样，您会发现一个简单的线性回归练习已解决，此外，还有一个简单的在线线性回归计算器。

什么是简单线性回归？

简单线性回归是一种用于关联自变量的统计模型，我们尝试近似两个变量之间的关系。

因此，简单线性回归用于查找将两个变量线性相关的方程。从逻辑上讲，两个变量之间的关系必须是线性的，否则必须使用另一种回归模型。

简单线性回归模型的方程由两个系数组成：方程常数 (b ₀ ) 和两个变量之间的相关系数 (b ₁ )。因此，简单线性回归模型的方程为 y=b ₀ +b ₁ x。

简单线性回归方程被绘制为一条直线，因此系数 b ₀是截距，系数 b ₁是直线的斜率。

简单线性回归公式

简单线性回归系数的计算公式如下：

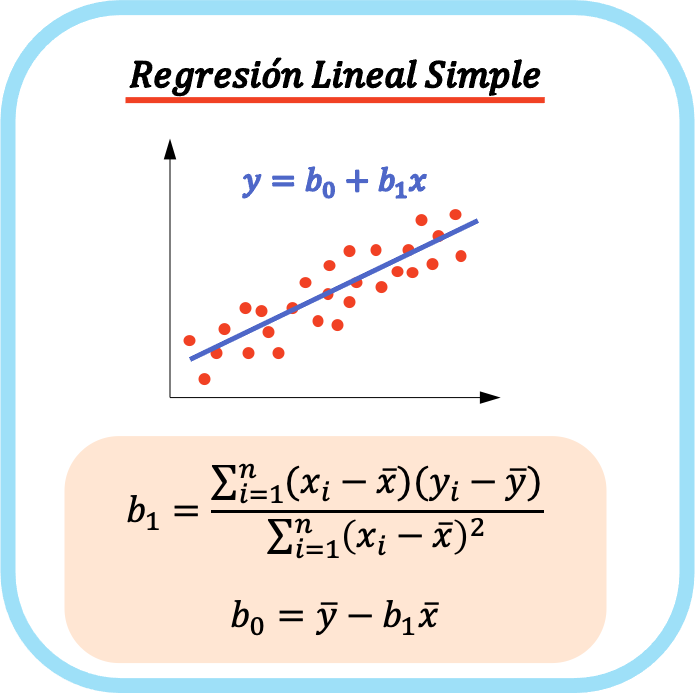
👉您可以使用下面的计算器来计算任何数据集的简单线性回归的系数。

显然，简单线性回归模型得出的方程将无法猜测所有观测值的准确值，因为该模型只是试图找到一个近似两个变量之间关系的方程。因此，残差被定义为真实值与线性回归模型估计值之间的差异。

请注意，简单线性回归模型的目标是最小化残差的平方，即简单线性回归基于最小二乘准则。

简单线性回归的具体示例

为了完成对简单线性回归方法的理解，这里有一个实际的分步示例，其中简单线性回归模型的方程是根据一组统计数据计算出来的。

• 参加统计考试后，五名学生被问及他们为考试投入了多少时间。数据如下表所示。对收集的统计数据执行简单的线性回归模型，将学习时间与取得的成绩线性相关。

为了建立简单的线性回归模型，我们必须确定方程的系数 b ₀和 b ₁ ，为此，我们必须使用上一节中看到的公式。

然而，要应用简单线性回归公式，我们必须首先计算自变量的均值和因变量的均值：

现在我们知道了变量的均值，我们使用相应的公式计算模型的系数 b ₁ ：

最后，我们使用相应的公式计算模型的系数b ₀ ：

简而言之，该问题的简单线性回归模型方程为：

下面您可以看到样本数据的图形表示以及简单线性回归模型的直线：

最后，一旦我们计算了简单线性回归模型的方程，剩下的就是解释所获得的结果。为此，必须计算回归模型的决定系数，您可以通过在我们的网站上搜索相应的文章来了解这是如何完成的。

简单线性回归假设

为了执行简单线性回归，必须满足以下假设：

• 独立性：观察到的残基必须相互独立。确保模型独立性的常见方法是在采样过程中添加随机性。
• 同方差性：残差的方差必须具有同质性，即残差的变异性必须恒定。
• 正态性：残差必须服从正态分布，换句话说，它们必须服从均值为 0 的正态分布。
• 线性——自变量和因变量之间的关系应该是线性的。

简单线性回归计算器

将样本数据插入下面的计算器中，以拟合两个变量之间的简单线性回归模型。您需要分离数据对，以便第一个框中只有自变量 X 的值，第二个框中只有因变量 Y 的值。

数据必须用空格分隔，并使用句点作为小数点分隔符输入。

简单和多元线性回归

最后，我们将了解简单线性回归和多元线性回归之间的区别，因为它们是统计学中经常使用的两种线性回归。

多元线性回归可以在数学上将两个或多个解释变量与响应变量联系起来。也就是说，在多元线性回归中，创建的模型中至少有两个自变量。

因此，简单线性回归和多元线性回归之间的区别在于自变量的数量。在一元线性回归中，只有一个自变量，而在多元线性回归中，有两个或多个自变量。