如何在 excel 中执行简单线性回归
简单线性回归是一种我们可以用来理解解释变量 x 和响应变量 y 之间关系的方法。
本教程介绍如何在 Excel 中执行简单的线性回归。
示例:Excel 中的简单线性回归
假设我们想要了解学生为考试学习的小时数与考试成绩之间的关系。
为了探索这种关系,我们可以使用学习时间作为解释变量,考试成绩作为响应变量来执行简单的线性回归。
在 Excel 中完成以下步骤以执行简单线性回归。
第 1 步:输入数据。
输入 20 名学生的学习时数和考试成绩的以下数据:
第 2 步:可视化数据。
在执行简单的线性回归之前,创建数据散点图会很有帮助,以确保学习时间和考试成绩之间确实存在线性关系。
突出显示 A 列和 B 列中的数据。沿着 Excel 的顶部功能区,导航到“插入”选项卡。在“图形”组中,单击“插入散点图 (X, Y)” ,然后单击标有“散点图”的第一个选项。这将自动生成以下点云:
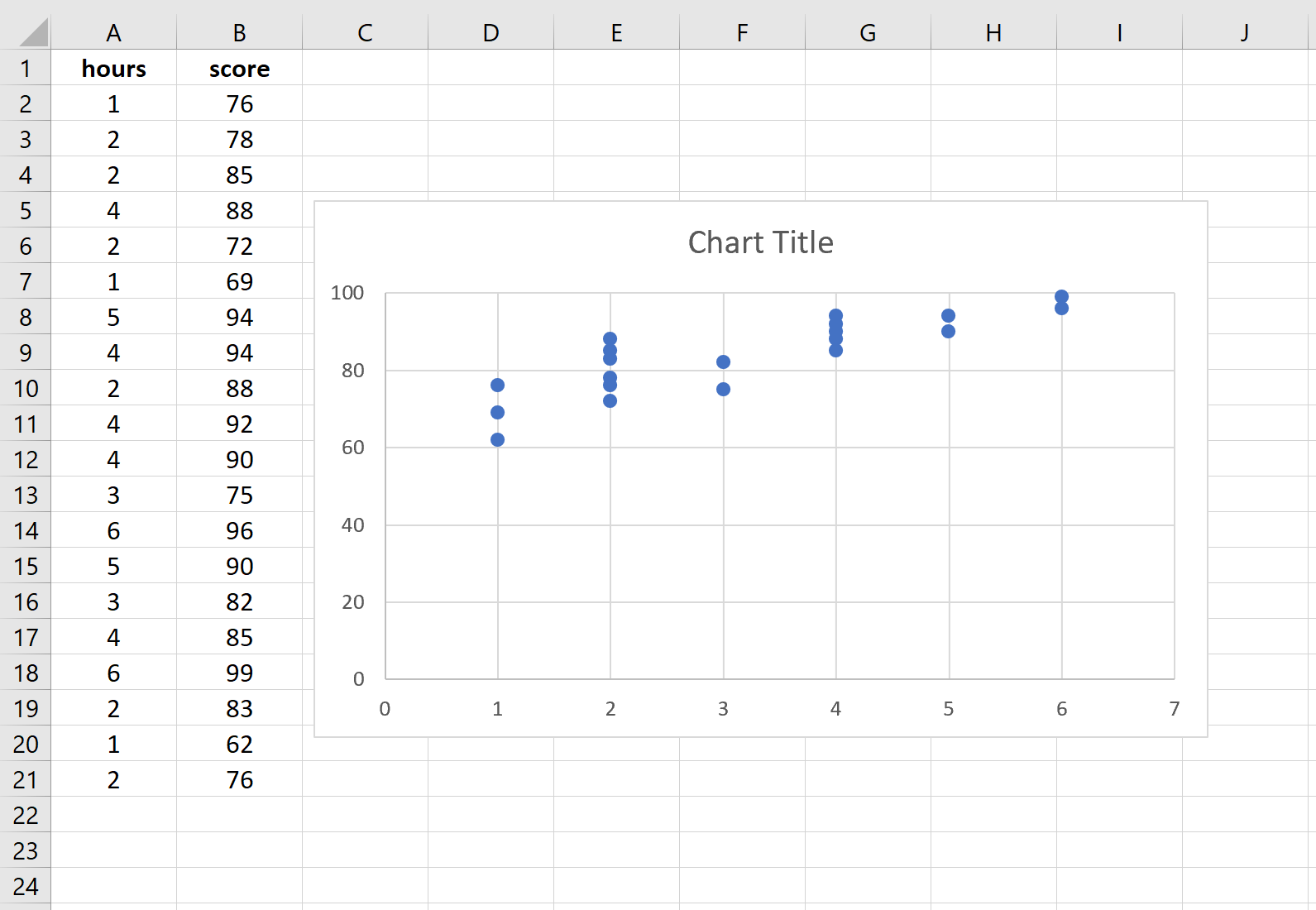
学习小时数显示在 x 轴上,考试结果显示在 y 轴上。我们可以看到这两个变量之间存在线性关系:学习时间越长,考试成绩越高。
为了量化这两个变量之间的关系,我们可以执行简单的线性回归。
步骤 3:执行简单线性回归。
在 Excel 的顶部功能区上,转到“数据”选项卡,然后单击“数据分析” 。如果您没有看到此选项,则必须首先安装免费的分析工具库软件。

单击“数据分析”后,将出现一个新窗口。选择回归并单击确定。
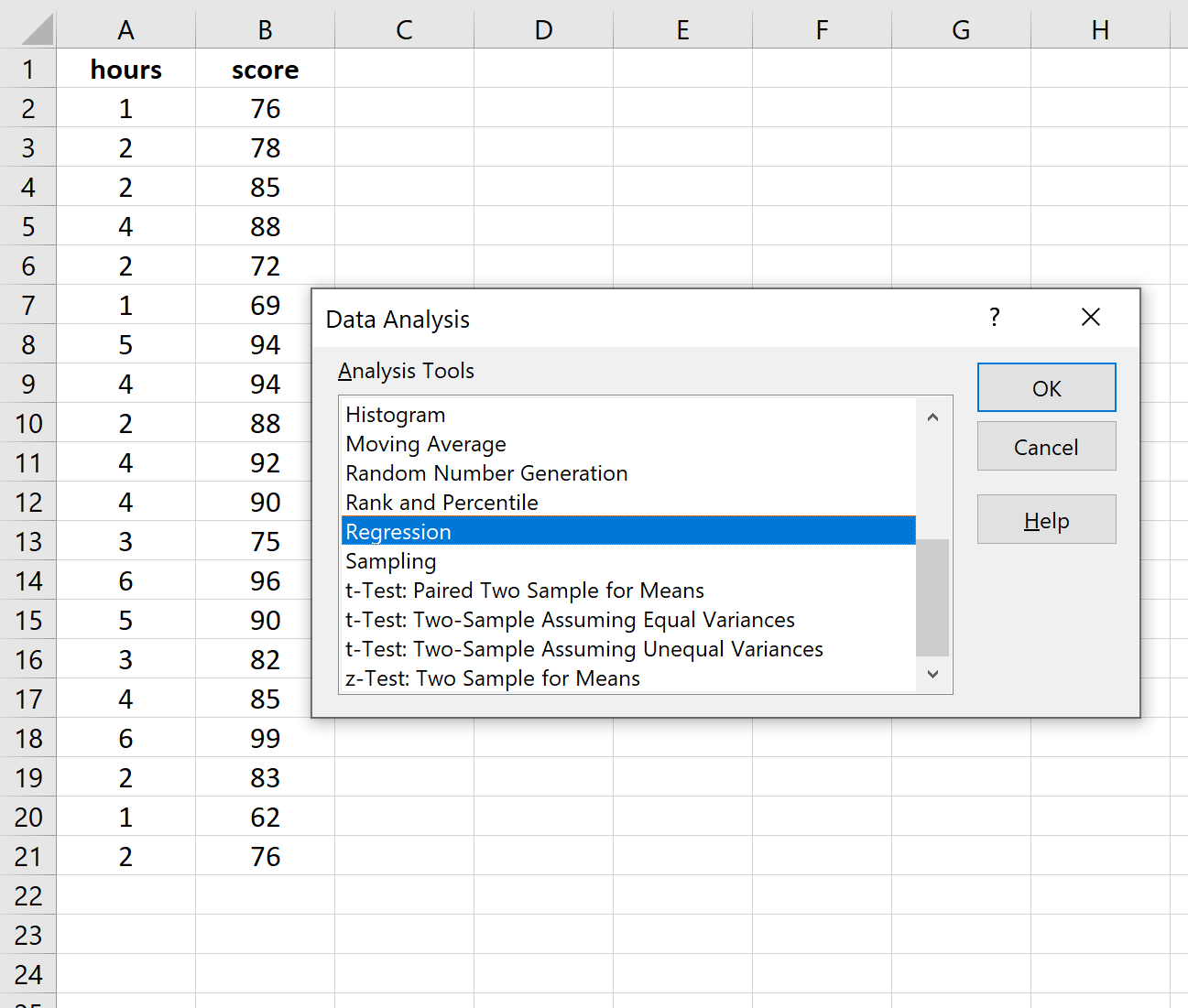
对于输入 Y 范围,填写响应变量的值数组。对于输入 X 范围,填写解释变量的值数组。
选中“标签”旁边的框,让 Excel 知道我们已将变量名称包含在输入范围中。
对于输出范围,选择要在其中显示回归输出的单元格。
然后单击“确定” 。
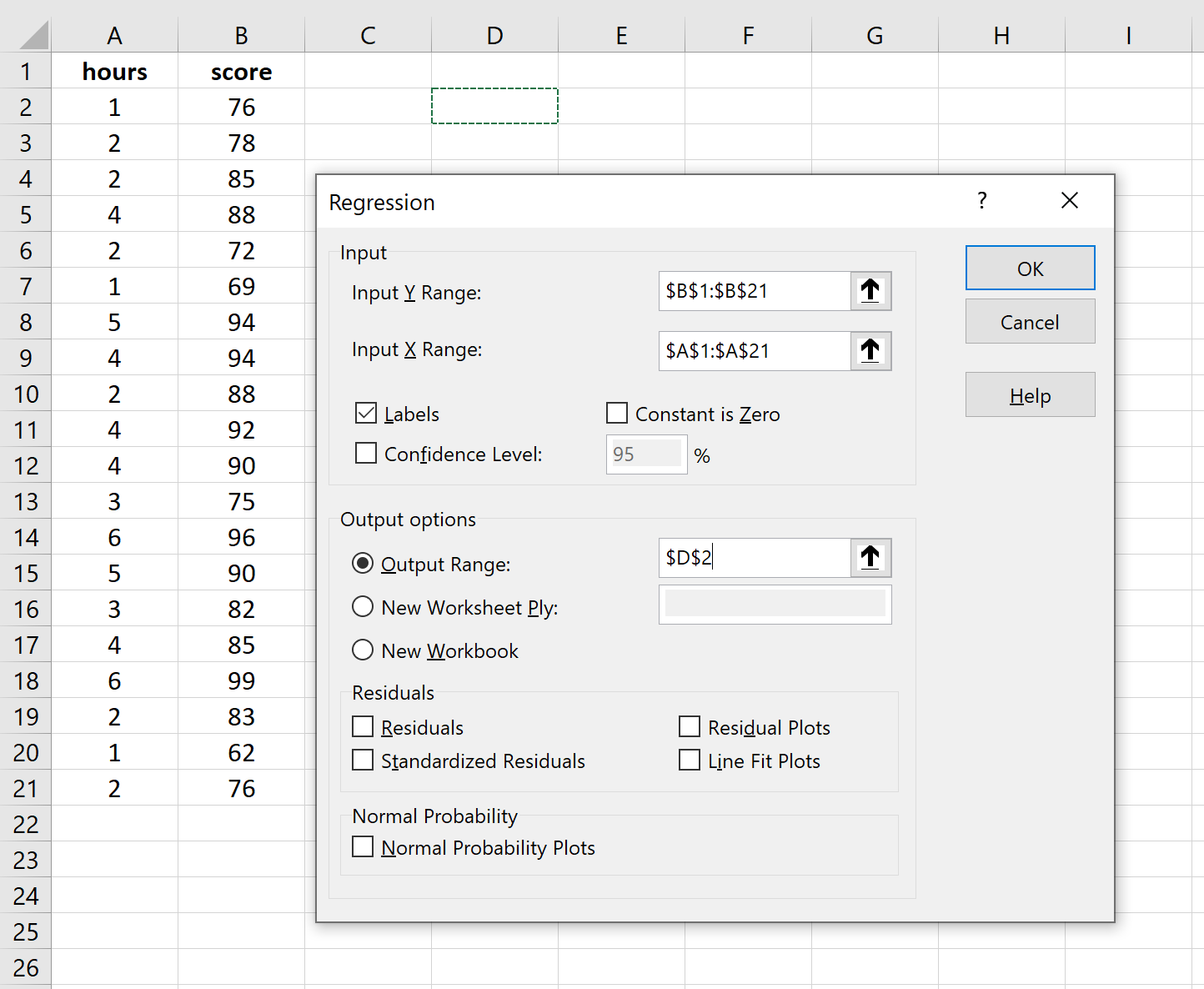
将自动出现以下输出:

步骤 4:解释结果。
以下是如何解释结果中最相关的数字:
R 方: 0.7273 。这称为决定系数。它是响应变量中可以由解释变量解释的方差的比例。在此示例中,72.73% 的考试成绩差异是由学习时数来解释的。
标准误差: 5.2805 。这是观测值与回归线之间的平均距离。在本例中,观测值与回归线平均偏差 5.2805 个单位。
F:47.9952 。这是回归模型的总体 F 统计量,计算方式为回归 MS/残余 MS。
含义 F:0.0000 。这是与总体 F 统计量相关的 p 值。这告诉我们回归模型是否具有统计显着性。换句话说,它告诉我们解释变量与响应变量是否具有统计上显着的关联。在这种情况下,p 值小于 0.05,表明学习时间与考试成绩之间存在统计显着关联。
系数:系数为我们提供了编写估计回归方程所需的数字。在本例中,估计回归方程为:
考试成绩 = 67.16 + 5.2503*(小时)
我们将学时系数解释为每多学习一小时,考试成绩平均应增加5.2503 。我们将截距系数解释为学习零小时的学生的预期考试成绩为67.16 。
我们可以使用这个估计的回归方程根据学习小时数计算学生的预期考试成绩。
例如,学习三个小时的学生应获得82.91的考试成绩:
考试成绩 = 67.16 + 5.2503*(3) = 82.91
其他资源
以下教程说明如何在 Excel 中执行其他常见任务: