算术平均

在这里我们解释什么是算术平均值以及它是如何计算的。您会找到算术平均值示例，甚至还有一个计算器来查找任何统计样本的算术平均值。最后，您将能够了解这种平均值的属性是什么，以及如何通过按区间分组的数据获得算术平均值。

算术平均值是多少？

算术平均值是一组统计数据的中心值特征。为了计算算术平均值，将所有值相加并除以数据总数。

此外，算术平均值是用于对样本进行统计研究的主要指标之一。

因此，算术平均值的公式如下：

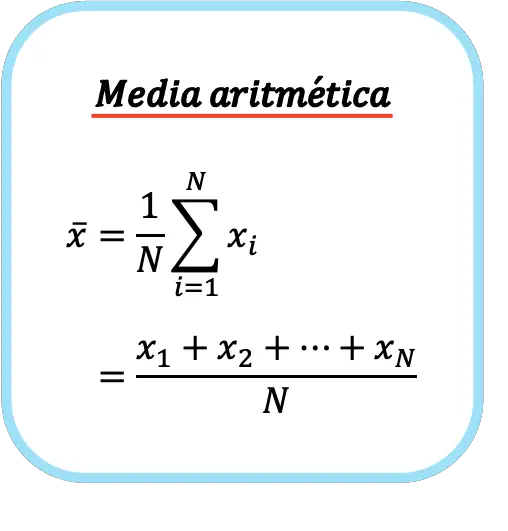
算术平均值的符号是字母 x 上方的水平带。

您还可以使用均值符号区分样本均值和总体均值：样本均值用符号表示

，另一方面，对于人口的平均值，我们使用希腊字母

应该注意的是，总体的算术平均值相当于统计变量的期望值。

算术平均数也称为算术平均数，它并不是唯一存在的平均数，还有加权平均数、平方平均数、几何平均数和调和平均数等。您可以在我们网站的搜索引擎中查看它们是如何计算的。

如何计算算术平均值

要计算算术平均值，必须执行以下步骤：

1. 添加样本中的所有统计数据。
2. 将先前的总和除以数据总数。
3. 所得结果为统计样本的算术平均值。

👉您可以使用下面的计算器来计算任何数据集的算术平均值。

计算算术平均值的示例

给出算术平均值的定义，我们将通过逐步求解示例来了解如何获得一组数据的算术平均值。

• 学生在学年中取得以下成绩：数学 9 分、语言 7 分、历史 6 分、经济学 8 分、科学 7.5 分。你所有成绩的算术平均数是多少？

为了求算术平均数，我们需要将所有成绩相加，然后除以课程的科目总数，即 5。因此，我们应用算术平均数公式：

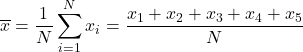
我们将数据代入公式并计算算术平均值：

可以看到，在算术平均中，对每个值赋予相同的权重，即每条数据在整体中具有相同的权重。

算术平均值计算器

将任何统计样本的数据输入以下计算器以计算其算术平均值。数据必须用空格分隔，并使用句点作为小数点分隔符输入。

分组数据的算术平均值

通过分组数据，我们的意思是数据被构造为组或间隔。当统计样本量非常大时，通常会发生这种情况。

因此，尽管概念相同，但当数据分组在一起时，算术平均值的计算略有不同。

要计算按区间分组的数据的算术平均值，必须将每组的班级分数乘以其绝对频率，然后除以所有绝对频率的总和。

为了让您了解这是如何完成的，下面是对按区间分组的数据的算术平均值的已解决练习：

• 我们想要统计研究一个群体的体重，为此我们采访了一个由 81 人组成的代表性群体，我们得到了以下数据：

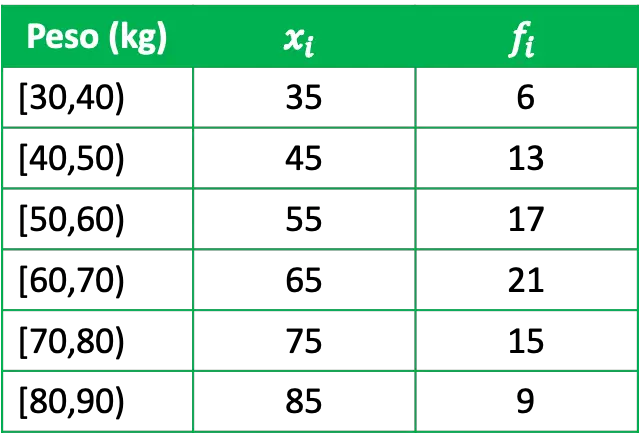
其中x _i为各组的班级分数，f _i为绝对频数，即在该区间内有权重的人数。

为了确定算术平均值，需要在频率表中添加一列，该列是类别音符与其各自绝对频率的乘积：

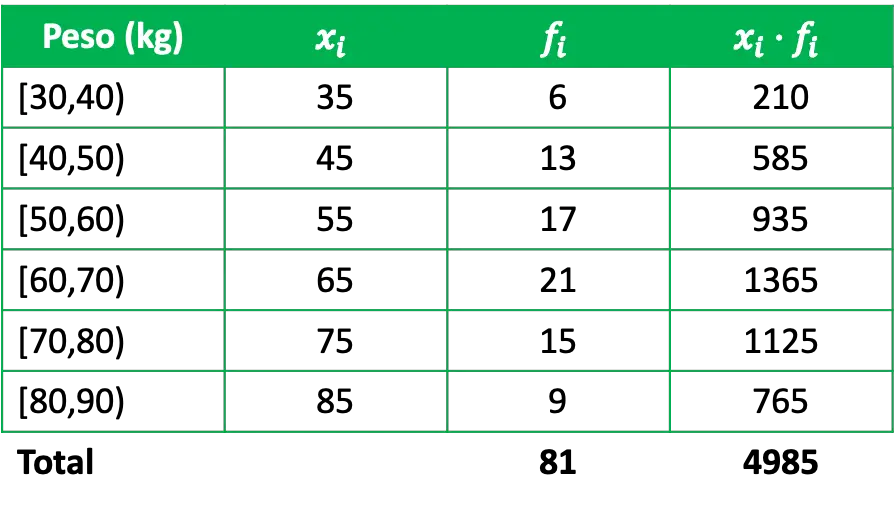
因此，要计算分组数据的算术平均值，只需将班级笔记除以频率的乘积之和除以数据总数即可：

算术平均值的性质

算术平均数具有以下特点：

• 分布中所有数据与平均值的偏差之和为零。

• 如果我们将相同的数量添加到样本中的所有数据中，则样本均值会增加该数量。

• 乘法也会发生同样的情况，如果将样本中的所有值乘以一个数字，则样本平均值将乘以该数字。

• 算术平均值只能计算定量变量。换句话说，你不能取定性变量的平均值。

• 算术平均值始终是分布的最小值和最大值之间的值。

• 这种类型的平均值对非常高或非常低的值非常敏感，导致异常值显着改变算术平均值的结果。

• 数据集的算术平均值始终等于或大于同一数据集的几何平均值。

用Excel计算算术平均值

在 Excel 中计算算术平均值非常简单，因为您只需在工作表上输入数据并使用AVERAGE函数即可。

例如，要确定我们解释的第一个已解决练习中数据的算术平均值，只需将所有数据复制到 Excel 文档中，并在单元格中写入以下公式： =AVERAGE(9;7;5; 8;7 ,5) .该函数将返回数据的算术平均值，即 7.3。

显然，用Excel程序求某些数字的算术平均值比手工计算要快得多，特别是当样本量很大时。