简单线性回归简介

简单线性回归是一种统计方法，可用于了解两个变量 x 和 y 之间的关系。

变量x称为预测变量。

另一个变量y称为响应变量。

例如，假设我们有以下数据集，其中包含七个人的体重和身高：

令体重为预测变量，身高为响应变量。

如果我们使用散点图绘制这两个变量，其中 x 轴为重量，y 轴为高度，则结果如下所示：

假设我们想了解体重和身高之间的关系。从散点图中我们可以清楚地看到，随着体重的增加，身高也趋于增加，但要真正量化体重和身高之间的这种关系，我们需要使用线性回归。

使用线性回归，我们可以找到最“适合”我们的数据的线。这条线被称为最小二乘回归线，可以用来帮助我们理解体重和身高之间的关系。

通常，您将使用 Microsoft Excel、SPSS 或图形计算器等软件来查找该直线的方程。

最佳拟合线的公式为：

ŷ = b ₀ + b ₁ x

其中 ŷ 是响应变量的预测值，b ₀是截距，b ₁是回归系数，x 是预测变量的值。

相关： 现实生活中使用线性回归的 4 个示例

找到“最适合的线路”

对于此示例，我们可以简单地将数据插入统计线性回归计算器并按计算：

计算器自动找到最小二乘回归线：

ŷ = 32.7830 + 0.2001x

如果我们缩小之前的散点图并将这条线添加到图表中，它会是这样的：

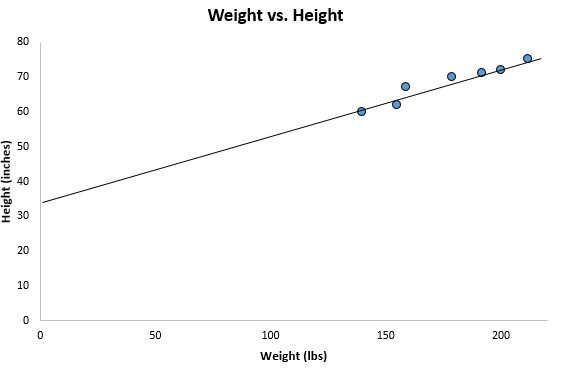
请注意我们的数据点是如何紧密分散在这条线周围的。事实上，这条最小二乘回归线是我们可以绘制的所有可能的线中最适合我们的数据的线。

如何解释最小二乘回归线

以下是如何解释这条最小二乘回归线： ŷ = 32.7830 + 0.2001x

_b0 = 32.7830 。这意味着当预测变量重量为零磅时，预测身高为 32.7830 英寸。有时，了解 b ₀的值可能很有用，但在这个特定示例中，解释 b ₀没有任何意义，因为一个人的体重不可能为零。

_b1 = 0.2001 。这意味着x增加 1 个单位与y增加 0.2001 个单位相关。在这种情况下，重量增加 1 磅与高度增加 0.2001 英寸相关。

如何使用最小二乘回归线

使用最小二乘回归线，我们可以回答以下问题：

对于体重 170 磅的人来说，我们应该期望他们有多高？

为了回答这个问题，我们可以简单地将 170 插入到 x 的回归线中并求解 y：

ŷ = 32.7830 + 0.2001(170) = 66.8 英寸

对于体重 150 磅的人，我们应该期望他们有多高？

为了回答这个问题，我们可以在 x 的回归线中插入 150 并求解 y：

ŷ = 32.7830 + 0.2001(150) = 62.798 英寸

注意：当使用回归方程回答此类问题时，请确保仅使用数据集中预测变量范围内的预测变量值。我们用来生成最小二乘回归线的原点。例如，我们数据集中的体重范围在 140 到 212 磅之间。因此，当体重在 140 至 212 磅之间时，回答有关预期身高的问题是有意义的。

决定系数

衡量最小二乘回归线“拟合”数据的程度的一种方法是使用决定系数，表示为 R ² 。

决定系数是响应变量中可由预测变量解释的方差的比例。

决定系数可以在 0 到 1 之间变化。值 0 表示响应变量根本无法由预测变量解释。值为 1 表示响应变量可以由预测变量完美解释，没有错误。

R ²介于 0 和 1 之间表示响应变量可以由预测变量解释的程度。例如，R ²为 0.2 表示响应变量中 20% 的方差可以由预测变量解释； R ²为 0.77 表示响应变量中 77% 的方差可以由预测变量解释。

请注意，在我们之前的结果中，我们获得的 R ²为 0.9311，这表明 93.11% 的身高变异性可以通过体重预测变量来解释：

这告诉我们体重是身高的一个很好的指标。

线性回归假设

为了使线性回归模型的结果有效且可靠，我们必须验证是否满足以下四个假设：

1.线性关系：自变量x和因变量y之间存在线性关系。

2. 独立性：残差是独立的。特别是，时间序列数据中的连续残差之间不存在相关性。

3.同方差性：残差在x的每个水平上具有恒定的方差。

4. 正态性：模型残差呈正态分布。

如果这些假设中的一个或多个不满足，那么我们的线性回归的结果可能不可靠，甚至具有误导性。

请参阅 本文，了解每个假设的解释、如何确定是否满足假设以及如果不满足假设该怎么办。