统计中的随机化:定义和示例
在统计学领域,随机化是指将研究对象随机分配到不同治疗组的行为。
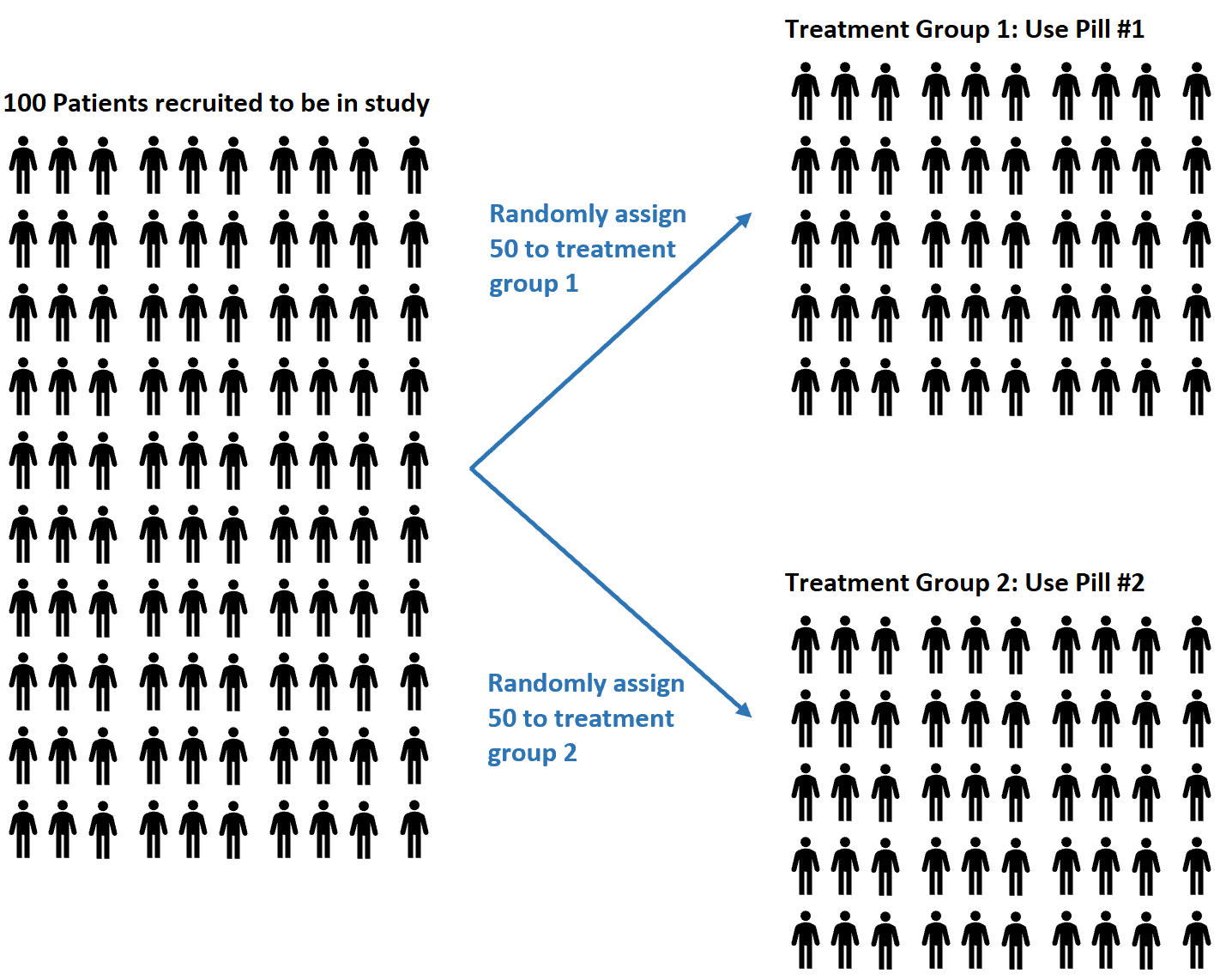
例如,假设研究人员招募 100 名受试者参加一项研究,他们希望了解两种不同的药物是否对血压有不同的影响。
他们可能决定使用随机数生成器来随机分配每个受试者使用#1 药丸或#2 药丸。
随机化的优点
随机化的目的是控制隐藏变量,即未直接包含在分析中但以某种方式影响分析的变量。
例如,如果研究人员研究两种不同药物对血压的影响,以下隐藏变量可能会影响分析:
- 燕尾服衣服
- 饮食
- 锻炼
通过将受试者随机分配到治疗组,我们最大限度地提高了隐藏变量对两个治疗组产生同等影响的机会。
这意味着血压的任何差异都可以归因于药物的类型,而不是隐藏变量的影响。
分组随机化
随机化的扩展称为块随机化。这是首先将受试者分成组,然后使用随机化将组内的受试者分配给不同治疗的过程。
例如,如果研究人员想知道两种不同的药物对血压的影响是否不同,他们可以首先根据性别将所有受试者分为两部分:男性或女性。
然后,在每个区块中,他们可以使用随机化来随机分配受试者使用#1 药丸或#2 药丸。
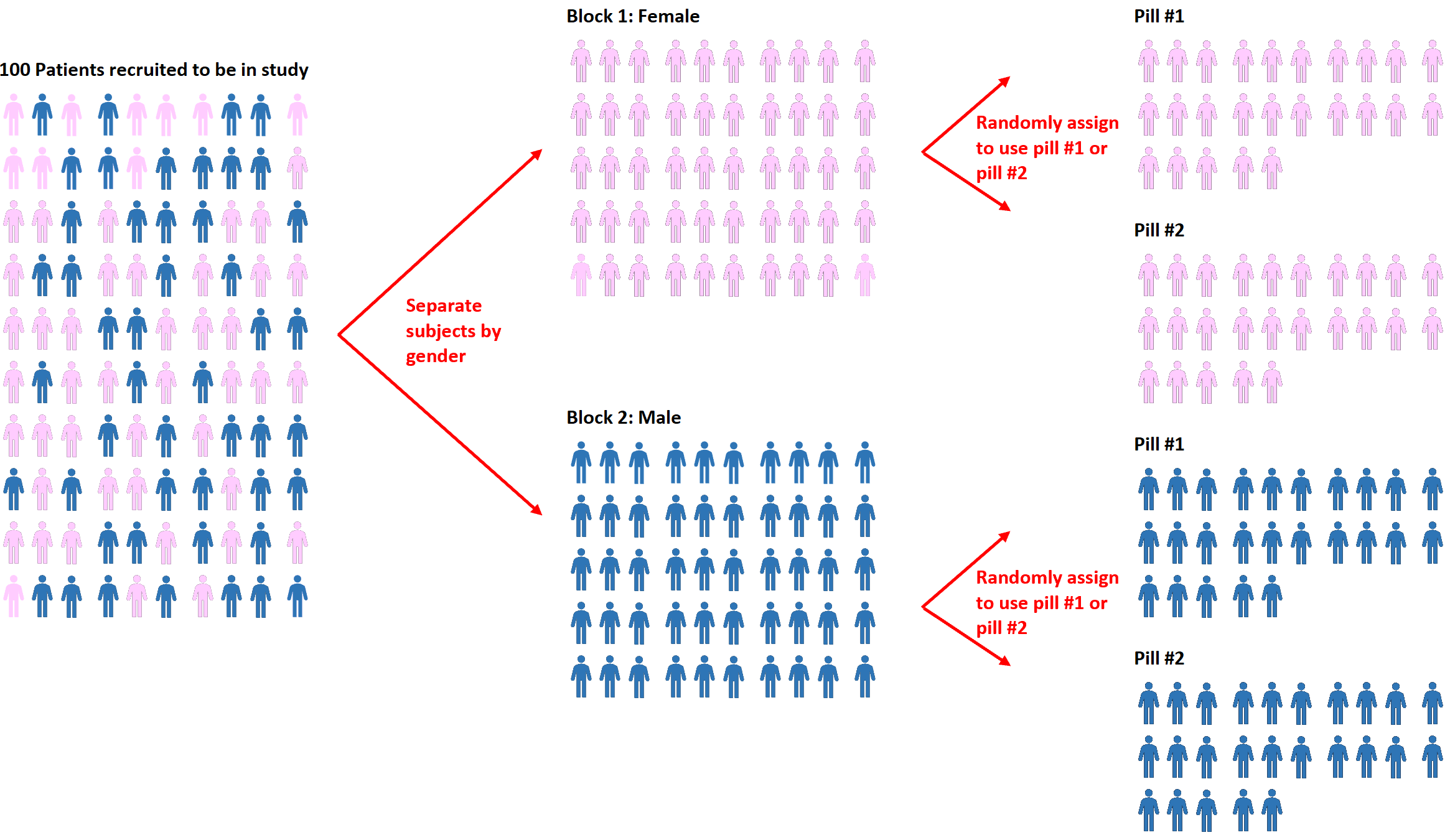
这种方法的优点是研究人员可以直接控制性别对血压可能产生的任何影响,因为我们知道男性和女性对每种药物的反应可能不同。
通过使用性别作为块,我们能够消除这个变量作为潜在的变异来源。如果两种药之间的血压存在差异,那么我们就可以知道性别并不是造成这些差异的根本原因。