统计样本

本文解释了什么是统计样本及其用途。您还将能够看到总体和样本概念之间的差异以及统计样本的几个示例。此外，它还显示了样本必须具备的代表性特征。

什么是统计样本？

统计样本是来自统计总体的一组个体。换句话说，在统计学中，样本是进行统计研究的总体的一部分。

例如，进行选举调查时，统计样本由所有接受调查的人组成。

通常，当我们想做研究时，我们不可能研究组成研究组的所有元素。就像前面的例子一样，不可能检查所有在选举中投票的人。因此，通常选择一个样本来仅分析研究组的一部分，然后将结果外推到整个组。

这可以通过统计推断来实现，因为它允许从样本结果中以非常小的误差范围确定总体参数。

样本和总体

在统计学中，总体是一组具有相似特征的元素，旨在对其进行统计研究。这个概念可以称为统计总体或简称为总体。

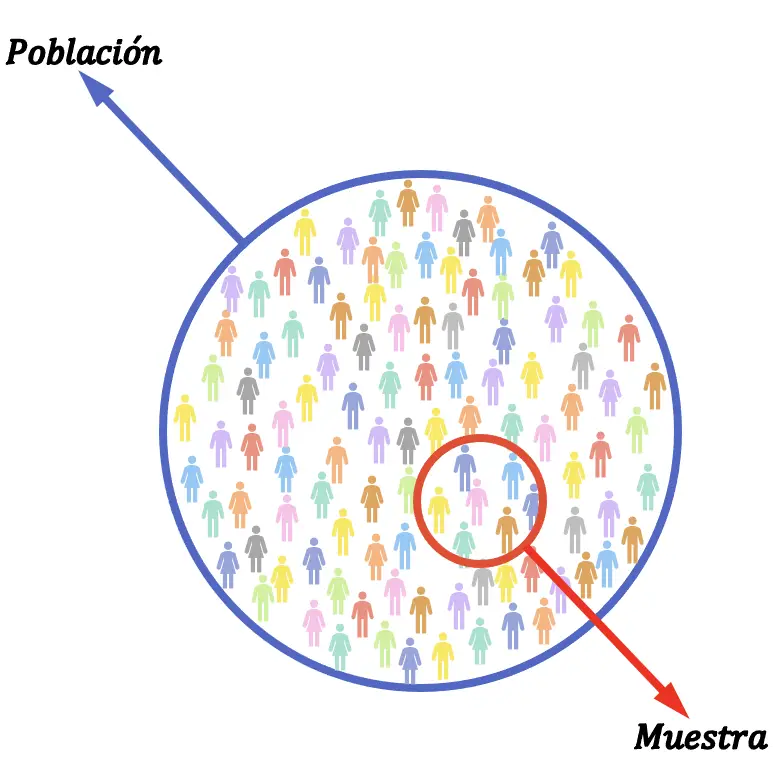
统计样本和统计总体之间的差异是相对于研究元素总数的比例，因为样本是总体的一部分，代表了构成要分析的群体的所有元素。

因此，样本的大小将始终小于或等于总体的大小。

例如，如果我们想对一家工厂生产的缺陷零件的比例进行统计研究，我们不会研究所有制造的零件，而只会研究随机选择的一组零件。因此，在这种情况下，总体由工厂生产的零件组成，另一方面，样本是统计研究中分析的所有零件。

重要的是，选择进行统计调查的样本能够代表总体的特征，以便从样本中得出的结论可以外推到整个总体。然后我们将了解如何从样本中选择个体。

样品与抽样

在统计学中，抽样是从总体中选择样本的过程。换句话说，抽样是选择一组个体进行统计研究的方法。

例如，进行抽样的一种方法是随机选择个体。因此，如果我们想研究统计总体的规模，我们可以通过简单随机抽样来选择研究样本。

有多种对总体进行抽样的方法，每种方法都有其优点和缺点。单击以下链接查看统计抽样的不同类型。

样本量

样本量（或样本量）是构成研究样本的个体数量。在统计学中，样本量很重要，这样样本才能代表整个总体。

例如，如果我们想对一个国家的身高进行分析，我们不能要求该国所有居民的身高，因为测量时间会很长，而且成本太高。因此，有必要进行随机抽样并仅采访总体中具有代表性的样本。

然而，统计研究的样本量必须足够大，才能代表整个人群的特征。另一方面，样本量不能太大，因为这样研究就会变得更加昂贵。因此，样本量要适当，不能太大也不能太小。您可以在此处了解如何计算适当的样本量：

代表性的样本

在统计学中，代表性样本是能够充分代表总体中个体的样本。换句话说，代表性样本是总体中的一部分，其特征与其所代表的总体的特征相似。

统计调查的样本具有代表性非常重要，这样所获得的结果才能适用于整个人口。如果研究的样本不具有代表性，则获得的结果将与总体不相符，从而得出错误的结论。

获得代表性样本的方法不能基于随机选择一组个体，而是样本的代表性取决于抽样方法、样本大小、误差幅度、置信度等几个因素， ETC。

首先，必须使用适当的抽样技术来获取有代表性的样本。抽样有多种类型，每种类型都适合一种样本类型，因此根据总体特征，最好使用一种抽样技术或另一种抽样技术。

在以下链接中，您可以了解不同类型的采样以及哪种类型最适合每种情况：

此外，您需要避免出现抽样错误。抽样误差是在获取样本的过程中发生的错误，导致样本的特征与总体的特征不同。因此，通过样本数据估计总体参数是不正确的。因此，必须注意抽样过程和所选的抽样方法。

其次，样本必须具有足够的代表性。为了使样本能够代表总体的属性，样本中的观测值数量必须足够大。另一方面，样本量不能太大，因为研究成本太高。总之，必须在代表性和样本成本之间取得平衡，选择理想的样本量。

统计中样本的优点

最后，让我们总结一下研究样本而不是整个总体的优势是什么：

• 仅检查样本使统计研究变得更容易，因为需要研究的个体更少。
• 由于收集数据的费用较少，因此研究的经济成本降低了。
• 这使得调查可以更快地进行，因为需要收集的数据更少。
• 它使得进行统计研究成为可能，而如果需要分析人口中的所有个体，则不可能进行这些研究。