时尚(统计)
本文解释了统计中的模式是什么。您将学习如何查找分组数据和未分组数据的统计模式、不同类型的模式以及此统计度量的几个示例。
统计学中的众数是什么?
在统计学中,众数是数据集中出现频率最高的值,即众数是数据集中重复次数最多的值。
因此,要计算统计数据集的众数,只需统计每个数据元素在样本中出现的次数,重复次数最多的数据就是众数。
众数用于定义统计分布,因为最重复的值通常位于分布的中心。
众数也可以说是统计众数或众数。类似地,当数据按区间分组时,最重复的区间是模态区间或模态类别。
一般情况下,术语Mo用作统计模式的符号,例如分布模式X为Mo(X)。
请记住,众数是中心位置以及中位数和平均值的统计度量。下面我们将了解每个统计指标的含义。
统计中的众数类型
在统计学中,有几种模式,根据最重复值的数量进行分类:
- 单峰模式:只有一个值具有最大重复次数。例如,[1,4,2,4,5,3]。
- 双峰模式:最大重复次数出现在两个不同的值处,并且两个值重复的次数相同。例如,[2,6,7,2,3,6,9]。
- 多峰模式:三个或更多值具有相同的最大重复次数。例如,[3,3,4,1,3,4,2,1,4,5,2,1]。
如何找到统计模式
要查找数据集的统计模式,必须执行以下步骤:
- 将数据按顺序排列。这一步不是强制性的,但它会让计数变得更容易。
- 计算每个数字出现的次数。
- 最常出现的数字是统计模式。
统计模式示例
考虑到统计学中时尚的定义,下面您可以看到每种时尚的示例,以便您更好地理解这个概念。
单峰模式示例
- 以下数据集的众数是什么?
![]()
数字没有排序,所以我们先对它们进行排序,以便更容易找到众数。
![]()
数字 2 和 9 出现了两次,但数字 5 重复了 3 次。因此,数据序列的众数为5。
![]()
双峰模式示例
- 计算以下数据集的众数:
![]()
![]()
首先我们把数字按顺序排列:
![]()
![]()
可以看到,数字6和数字8总共出现了四次,这是最大的重复次数。因此,在这种情况下它是双峰模式,两个数字是数据集的模式:
![]()
多模式示例
- 找到以下数据集模式:
![]()
![]()
![]()
由于数据较多,我们先将其按升序排序,以便于统计:
![]()
![]()
![]()
重复次数最多的数字是 20、27 和 31,这三个数字都重复了五次。因此,该示例的模式是多模式的。
![]()
时尚计算器
将任何统计样本的数据输入以下在线计算器以计算其众数。数据必须用空格分隔,并使用句点作为小数点分隔符输入。
分组数据模式
当我们将数据以区间形式分组时,我们并不真正知道每条数据重复了多少次,我们只知道每个区间的频率。
因此,要计算按区间分组的数据众数,我们必须使用以下公式:
![]()
金子:
- Li是模态区间的下限(最高绝对频率区间)。
- f i是模态区间的绝对频率。
- f i-1是模态之前间隔的绝对频率。
- f i+1是模态之后间隔的绝对频率。
- A i是模态区间的宽度。
作为示例,下面您解决了一个练习,其中计算分组为间隔的数据众数:
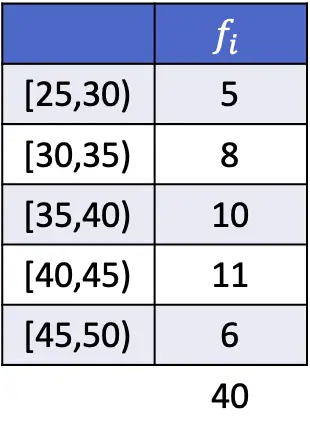
在本例中,模态区间为 [40,45),因为它是绝对频率最大的区间。因此,分组数据的众数公式参数为:
![Rendered by QuickLaTeX.com \begin{array}{c}L_i=40\\[2ex]f_i=11\\[2ex]f_{i-1}=10\\[2ex]f_{i+1}=6\\[2ex]A_i=5\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-85aef7092d3e0c7769ad17b96aae294c_l3.png)
因此,我们应用公式来确定按区间分组的数据的众数,并进行计算:
![Rendered by QuickLaTeX.com \begin{aligned}Mo & =L_i+ \cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i\\[2ex]& =40+ \cfrac{11-10}{(11-10)+(11-6)}\cdot 5\\[2ex]&=40,83\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-3ee33fdb43267fdcfc6d222ed6798fca_l3.png)
众数、平均值和中位数之间的差异
在最后一节中,我们将了解众数、均值和中位数之间的区别。由于这三者都是中心地位的统计指标,因此它们的含义是不同的。
正如整篇文章所解释的,数学中的众数是数据集中重复次数最多的值。
其次,平均值是所有统计数据的平均值。因此,要获得某些数据的平均值,必须将所有数据相加,然后将结果除以观测值数量。
最后,中位数是数据排序时占据中心位置的值。
因此,这三个统计指标有助于定义概率分布,因为它们提供了其中心值的想法。但请记住,没有一种衡量标准比另一种更好,它们只是意味着不同的概念。
时尚属性
时尚属性有:
- 众数可以在定量变量和定性变量中找到。
- 如果我们对随机变量应用线性变换,平均值的值将根据所应用的操作而变化。
- 一般来说,众数对异常值不敏感。
- 如果所有值的频率相同,则没有众数。
![]()