排名(统计)
在本文中,我们将解释统计中的范围是什么以及它是如何计算的。您将找到有关数据集范围的已解决练习,最后,我们将向您展示它的用途以及何时使用它。
统计学中的极差是什么?
在统计学中,极差是离散度的度量,表示样本数据的最大值和最小值之间的差异。因此,要计算总体或统计样本的范围,必须从最小值中减去最大值。
例如,如果一个数据集的最大值为9,最小值为2,则该统计样本的范围为7(9-2=7)。
统计范围也称为测量范围或范围。
因此,极差是用方差、标准差(或标准差)、平均差和变异系数来衡量离差的指标。
统计中如何计算极差
样本的极差是通过减去统计样本数据的极值来计算的,即样本的极差等于所有数据的最大值减去最小值。
因此,计算数据集统计极差的公式为:
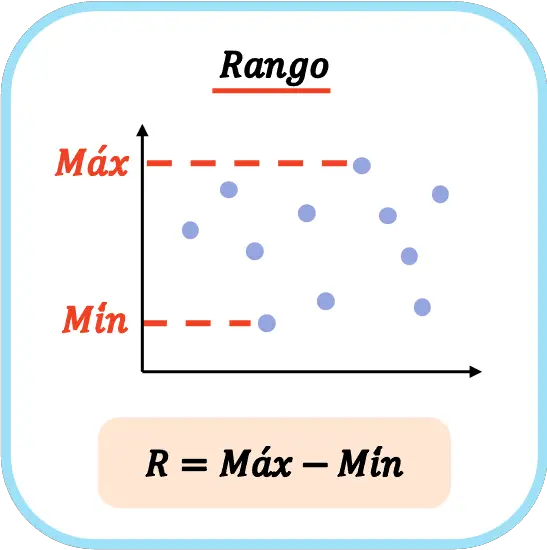
在统计学中,大写 R 的符号通常用于表示数据序列的范围。
因此,计算数据集的范围非常简单,因为您只需要确定极值之间的差异。您唯一需要注意的是正确获取最大和最小数据,并且不要忘记任何数字。
示例范围(统计)
了解统计中范围的定义后,下面是一个工作示例,以便您了解如何获取数据集的范围。
- 一家公司想要统计分析其旗舰产品在过去二十年中取得的销售额。为此,他们要求您计算一些统计指标,包括排名。如果产品的销量如下表所示,这个数据集的范围是多少?
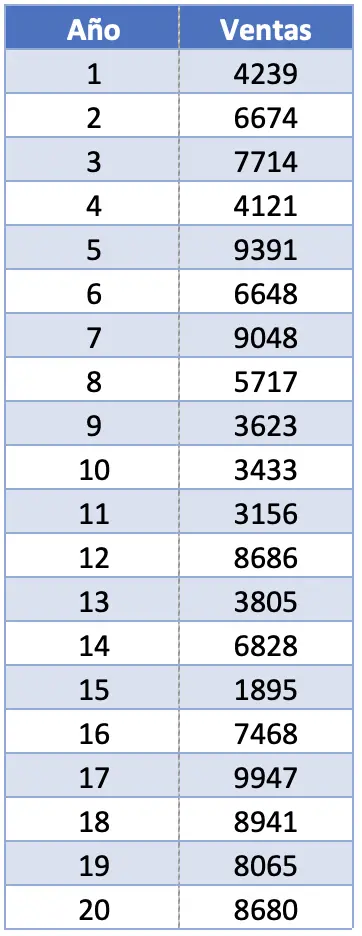
在本练习中,我们有 20 个观察结果。实际上,观测总数对于计算样本范围没有影响,因为我们只对最大值和最小值感兴趣。
因此,我们必须使用上面看到的公式来找到这个统计样本的范围。
![]()
区间的最大值为 9947 售出单位,最小值为 1895。因此,我们需要减去这两个值来找到数据集的范围:
![]()
这意味着过去几年销量的最大变化为8,052辆。下面您可以以图形方式查看所有运动数据及其统计范围,该图可能会帮助您理解范围的含义。
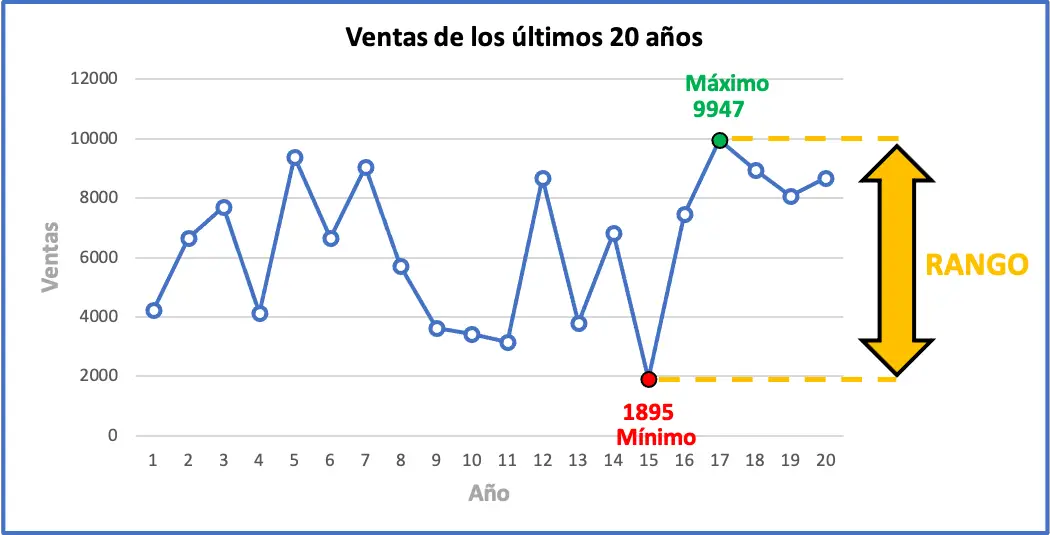
统计范围的用途是什么?
为了完全理解统计学中范围的概念,我们将了解它的用途以及如何解释这种离散度的度量。
在统计学中,极差表示数据集的最大值和最小值之间的差异。因此,极差是用来表示数据集总体离散程度的度量。
当您知道数据集的极差值时,您就知道该数据集中任意两个观测值之间的最大差异,因此您可以了解数据是否分散或靠近。一般来说,范围尽可能小是有利的,因为这意味着离散度很小,因此计算会更准确。
例如,范围可以是允许比较两个不同样本的测量值,因为它可以让您了解样本的分散情况。
然而,在解释统计范围时应谨慎,因为它可能会产生误导。可能数据集实际上具有非常低的离散度,但如果样本内存在异常值,则范围将非常宽,因此无法正确反映样本的离散度。
此外,数值为十量级的样本的排名为 5 与数值为数千量级的样本具有相同的排名是不一样的。从逻辑上讲,即使两个范围具有相同的数字,第一个样本也比第二个样本分散得多。
总之,极差是分析数据集分散性的有用统计指标,但为了正确解释数据,还必须计算其他指标。