频率(统计)
本文解释了统计学中频率的概念。因此,您将找到统计中频率的定义、存在的不同类型的频率,以及最后如何创建频率表。
统计学中的频率是什么?
在统计学中,频率是一个值在数据集中出现的次数。简而言之,频率是某个值在统计样本中重复的次数。
例如,如果在一项调查中,有 5 个人回答说他们最喜欢的颜色是蓝色,那么蓝色的频率就等于 5。
通常,在统计学中,用索引为i的字母f来表示值i的频率,因此频率的符号为fi 。
所有频率的总和给出了样本中数据的总数。因此,以下公式对于任何统计研究始终有效:
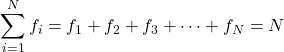
金子
![]()
是值的频率
![]()
和
![]()
是观测值的总数。
统计中的频率类型
在统计中,不同类型的频率如下:
- 绝对频率:对应于某个值在统计样本中出现的次数。
- 累积绝对频率:通过将值的绝对频率加上所有较小值的绝对频率相加来计算。
- 相对频率:这是绝对频率除以数据总数。
- 累积相对频率:等于该值的相对频率加上所有较低值的相对频率之和。
在下面的部分中,您可以看到每种频率类型的计算方式。
频率表
通常在统计学中,数据样本的频率计算总结在频率表中。下面是一个分步示例,您可以了解如何操作。
- 班级 30 名学生的统计科目成绩如下。构建数据集的频率表。
![]()
![]()
![]()
由于所有数字只能是整数,因此它是离散变量。因此,没有必要将数据分组为区间。
因此,我们需要构建一个表,其中每个不同的值都是一行。此外,我们需要找到每个值的绝对频率,为此,只需计算该值在数据样本中出现的次数即可。

请注意,所有绝对频率的总和等于数据总数。如果不遵守此规则,则意味着您忘记提供某些信息。
现在我们知道了绝对频率,我们需要找到累积绝对频率。对于此计算,我们有两种选择:要么将值的绝对频率加上最小值的所有绝对频率相加,要么相反,将值的绝对频率加上前一个值的累积绝对频率相加。

最后一个值的累积绝对频率始终对应于数据总数,您可以使用此技巧来验证计算是否正确。
接下来,我们需要确定相对频率,其计算方法是用绝对频率除以数据点总数 (30):

请记住,所有相对频率的总和始终等于 1,否则意味着频率表中的某些计算是错误的。
最后,提取累积的相对频率就足够了。为此,您必须将相关值的相对频率加上所有先前的相对频率,或者,相当于先前累积的相对频率:

简而言之,包含有问题数据的所有频率的频率表如下:
