方差分析的组内或组间变异
单向方差分析用于确定三个或更多独立组的平均值是否相等。
单向方差分析使用以下原假设和备择假设:
- H 0 :所有组平均值相等。
- H A :至少一组平均值与其他组不同。
每次执行单向方差分析时,您最终都会得到一个如下所示的汇总表:
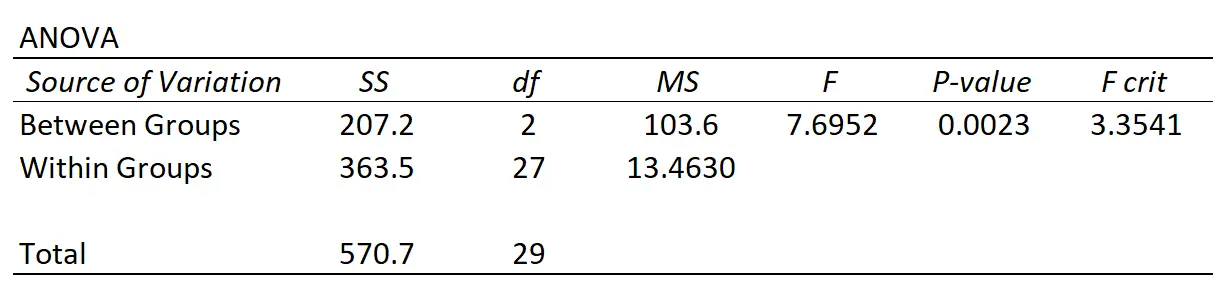
我们可以看到方差分析测量了两种不同的变异来源:
组间变异:各组平均值与总体平均值之间的总变异。
组内变异:每组中个体值的总变异及其组平均值。
如果组间变异相对于组内变异较大,则方差分析的 F 统计量会较高,相应的 p 值会较低,从而更有可能拒绝原假设,根据该假设组均值相等。
以下示例展示了如何在实践中计算单向方差分析的组间变异和组内变异。
示例:在方差分析中计算组内和组间的变异
假设我们想要确定三种不同的学习方法是否会导致不同的平均考试成绩。为了测试这一点,我们招募了 30 名学生,并随机分配每人 10人使用不同的学习方法。
各组学生考试成绩如下:
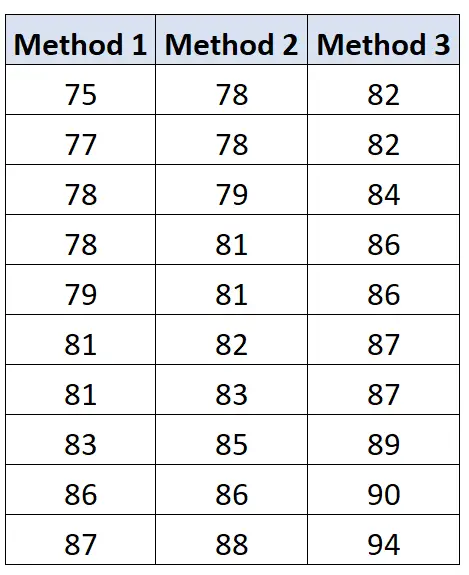
我们可以使用以下公式来计算组之间的变异:
组间变异= Σn j (X j – X ..) 2
金子:
- n j : 第 j 组的样本量
- Σ :表示“和”的符号
- X j : 第 j 组的平均值
- X .. : 总体平均值
为了计算这个值,我们首先计算每组的平均值和总体平均值:
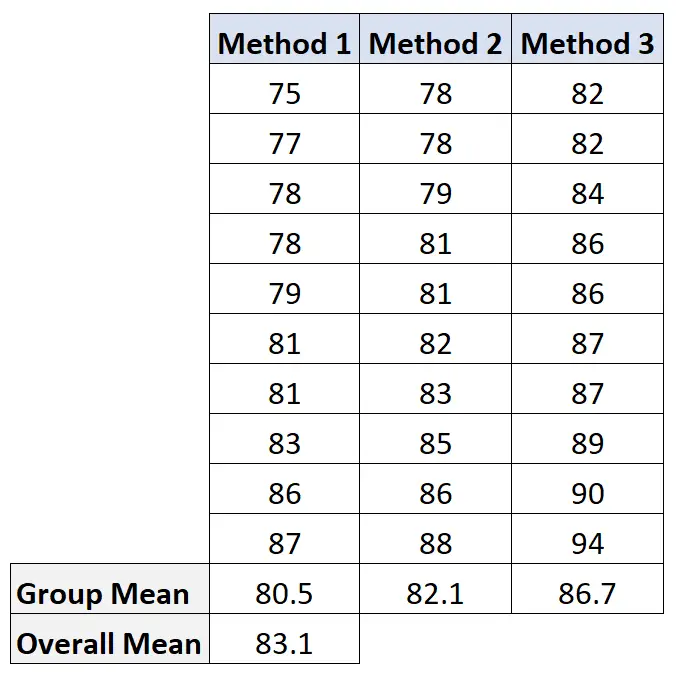
然后我们计算组之间的变异如下: 10(80.5-83.1) 2 + 10(82.1-83.1) 2 + 10(86.7-83.1) 2 = 207.2 。
然后我们可以使用以下公式来计算组内变异:
组内变异:Σ(X ij – X j ) 2
金子:
- Σ :表示“和”的符号
- X ij : j 组的第 i 个观察值
- X j : 第 j 组的平均值
在我们的示例中,我们计算组内的变异:
第 1 组: (75-80.5) 2 + (77-80.5) 2 + (78-80.5) 2 + (78-80.5) 2 + (79-80.5) 2 + (81-80.5) 2 + (81-80.5) 2 + (83-80.5) 2 + (86-80.5) 2 + (87-80.5) 2 = 136.5
第 2 组: (78-82.1) 2 + (78-82.1) 2 + (79-82.1) 2 + (81-82.1) 2 + (81-82.1) 2 + (82-82.1) 2 + (83-82.1) 2 + (85-82.1) 2 + (86-82.1) 2 + (88-82.1) 2 = 104.9
第 3 组: (82-86.7) 2 + (82-86.7) 2 + (84-86.7) 2 + (86-86.7) 2 + (86-86.7) 2 + (87-86.7) 2 + (87-86.7) 2 + (89-86.7) 2 + (90-86.7) 2 + (94-86.7) 2 = 122.1
组内变异: 136.5 + 104.9 + 122.1 = 363.5
如果我们使用统计软件使用该数据集进行单向方差分析,我们将得到以下方差分析表:
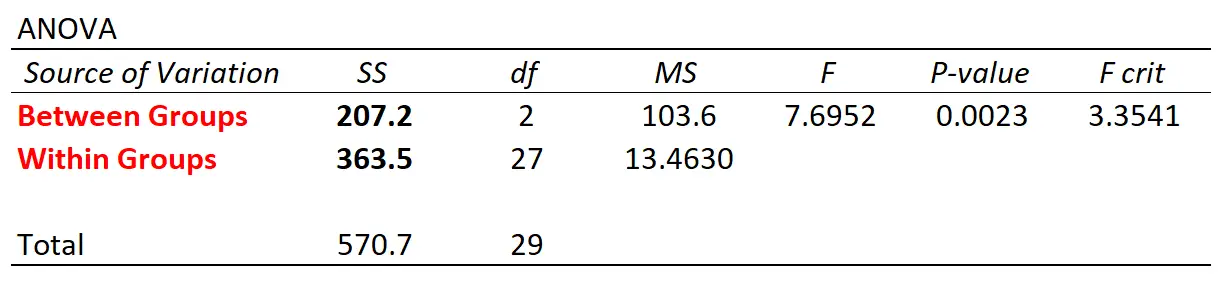
请注意,组间和组内变异值与我们手动计算的值相匹配。
表中的总体F统计量是量化组间变异和组内变异之间关系的一种方法。
F 统计量越大,组间的变异相对于组内的变异就越大。
所以,F统计量越大,说明组均值之间存在差异越明显。
我们可以在此示例中看到,与 F 统计量 7.6952 对应的 p 值为.0023 。
由于该值小于 α = 0.05,因此我们拒绝方差分析的原假设,并得出结论:三种学习技术不会导致考试得分相同。
其他资源
以下教程提供有关 ANOVA 模型的其他信息: